
【题目】某高中一年级600名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成![]() 组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
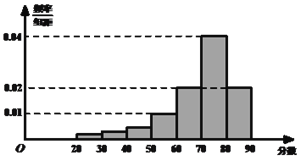
(1)从总体的600名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
【答案】(1)0.4(2)![]() (3)
(3)![]() .
.
【解析】试题分析:(1)根据频率=组距×高,可得分数小于70的概率;(2)先计算样本中分数不小于50的频率,进而计算可估计总体中分数在区间[40,50)内的人数;(3)先计算样本中分数不小于70的学生人数,即可算出样本中分数不小于70的男生人数,进而得到答案.
试题解析:(1)(0.02+0.04)×10=0.6,1-0.6=0.4 样本分数小于70的频率为0.4
∴总体中随机抽取一人,其分数小于70的概率估计为0.4
(2)根据题意,样本中分数不小于50的频率为![]() ,分数在区间
,分数在区间![]() 内的人数为
内的人数为![]() .
.
∴总体中分数在区间![]() 内的人数估计为
内的人数估计为![]() .
.
(3)由题意可知,样本中分数不小于70的学生人数为![]()
∴样本中分数不小于70的男生人数为![]()
∴样本中的男生人数为![]() ,女生人数为
,女生人数为![]() ,男生和女生人数的比例为
,男生和女生人数的比例为![]() .
.
∴根据分层抽样原理,总体中男生和女生人数的比例估计为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 种商品的概率为
种商品的概率为![]() .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量![]() 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届吉林省普通中学高三第二次调研】某校冬令营有三名男同学A,B,C和三名女同学X,Y,Z,
(1)从6人中抽取2人参加知识竞赛,求抽取的2人都是男生的概率;
(2)若从这3名男生和3名女生中各任选一名,求这2人中包含A且不包含X的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856332)
已知三棱柱ABC-A1B1C1如图所示,其中CA⊥平面ABB1A1,四边形ABB1A1为菱形,∠AA1B1=60°,E为BB1的中点,F为CB1的中点.
(Ⅰ)证明:平面AEF⊥平面CAA1C1;
(Ⅱ)若CA=2,AA1=4,求B1到平面AEF的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,其中
,其中![]() (e为椭圆离心率),焦距为2,过点M(4,0)的直线l与椭圆C交于点A,B,点B在AM之间.又点A,B的中点横坐标为
(e为椭圆离心率),焦距为2,过点M(4,0)的直线l与椭圆C交于点A,B,点B在AM之间.又点A,B的中点横坐标为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=![]() 在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为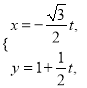 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com