
【题目】已知函数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的最小值;
的最小值;
(3)证明:当![]() 时,
时,![]() .
.
【答案】(1) 函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2) ![]() 的最小值为
的最小值为![]() .
.
(3)证明见解析.
【解析】分析:函数![]() 的定义域为
的定义域为![]() ,
,
(1)函数![]() ,据此可知函数
,据此可知函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
(2)由题意可知![]() 在
在![]() 上恒成立.据此讨论可得
上恒成立.据此讨论可得![]() 的最小值为
的最小值为![]() .
.
(3)问题等价于![]() .构造函数
.构造函数![]() ,则
,则![]() 取最小值
取最小值![]() .
.
设![]() ,则
,则![]() .由于
.由于![]() ,据此可知题中的结论成立.
,据此可知题中的结论成立.
详解:函数![]() 的定义域为
的定义域为![]() ,
,
(1)函数![]() ,
,
当![]() 且
且![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,
,
单调递增区间是![]()
(2)因在![]() 上
上![]() 为减函数,
为减函数,
故![]() 在
在![]() 上恒成立.
上恒成立.
所以当![]() 时,
时,![]() ,
,
又![]() ,
,
故当![]() ,即
,即![]() 时,
时,![]() .
.
所以![]() ,于是
,于是![]() ,
,
故![]() 的最小值为
的最小值为![]() .
.
(3)问题等价于![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
设![]() ,则
,则![]() ,
,
知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
故当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月11时的平均气温低于乙地该月11时的平均气温
②甲地该月11时的平均气温高于乙地该月11时的平均气温
③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差
④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差
其中根据茎叶图能得到的正确结论的编号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有![]() 、
、![]() 两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
|
| 总计 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
总计 | 36 | 64 | 100 |
(1)根据以上数据判断是有![]() 的把握认为招聘的
的把握认为招聘的![]() 、
、![]() 两个岗位与性别有关?
两个岗位与性别有关?
(2)从投简历的女生中随机抽取两人,记其中投![]() 岗位的人数为
岗位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,由上下两部分组成,上部的形状是正四棱锥![]() ,下部的形状是正四棱柱
,下部的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 是正四棱锥的高
是正四棱锥的高![]() 的4倍.
的4倍.

(1)若![]() ,
,![]() ,则仓库的容积是多少?
,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为![]() ,当
,当![]() 为多少时,下部的正四棱柱侧面积最大,最大面积是多少?
为多少时,下部的正四棱柱侧面积最大,最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ACBD(图①)中,△ABC与△ABD均为直角三角形且有公共斜边AB,设AB=2,∠BAD=30°,∠BAC=45°,将△ABC沿AB折起,构成如图②所示的三棱锥C′﹣ABC,且使 ![]() .
.
(Ⅰ)求证:平面C′AB⊥平面DAB;
(Ⅱ)求二面角A﹣C′D﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),……,第八组[190.195],下图是按上述分组方法得到的频率分布直方图.
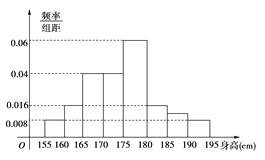
(1)求第七组的频数;
(2)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:

(1)求频率分布直方图中![]() 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数
的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数![]() 和中位数
和中位数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com