
分析 (1)利用极坐标方程的转化方法,可得结论;
(2)直线l的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}\right.(t$为参数),将$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}\right.$代入$\frac{x^2}{2}+{y^2}=1$得(cos2α+2sin2α)t2+2tcosα-1=0,利用参数的几何意义,即可求|PA|•|PB|的取值范围.
解答 解:(1)由$ρ=\sqrt{\frac{2}{{1+{{sin}^2}θ}}}$得ρ2(1+sin2θ)=2,得曲线C的普通方程为$\frac{x^2}{2}+{y^2}=1$.
(2)由题意知,直线l的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}\right.(t$为参数),将$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}\right.$代入$\frac{x^2}{2}+{y^2}=1$得(cos2α+2sin2α)t2+2tcosα-1=0,
设A,B对应的参数分别为t1,t2,
则$|{PA}|•|{PB}|=|{{t_1}{t_2}}|=\frac{1}{{{{cos}^2}α+2{{sin}^2}α}}=\frac{1}{{1+{{sin}^2}α}}∈[{\frac{1}{2},1}]$,
∴|PA|•|PB|的取值范围为$[{\frac{1}{2},1}]$.
点评 本题考查极坐标方程的转化,考查参数方程的运用,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
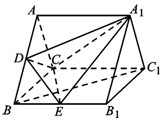 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
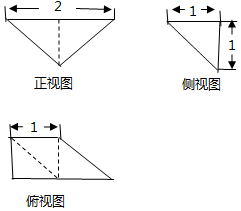 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )| A. | $\frac{1}{2}c{m^3}$ | B. | 1cm3 | C. | $\frac{3}{2}c{m^3}$ | D. | 3cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
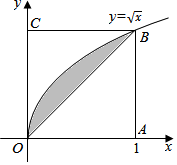 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,$\frac{{e}^{2}}{4}$) | C. | (0,e) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com