
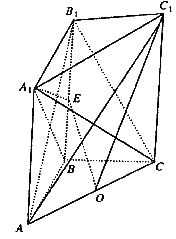
直三棱柱ABC―A1B1Cl中,已知AB=BC=2,∠ABC=90°,异面直线AlB与AC成60°角,点O、E分别为AC、BBl的中点.
(Ⅰ)求证:OE∥平面AB1Cl;
(Ⅱ)求证:A1E⊥OC1;
(Ⅲ)求二面角B1一A1C-Cl的大小.
解:(Ⅰ)证明:取ClC的中点F.连结EF、OF,则
 OF//AC1,EF//Bl C1
OF//AC1,EF//Bl C1
∴OF∥面ABlC1 EF∥面ABlC1.
∵EF![]() OF=F,ACl
OF=F,ACl ![]() BCl=C1
BCl=C1
∴平面OEF//平面AB1C1
又∵OE![]() 平面OEF
平面OEF
∴OE∥平面ABlC1
(Ⅱ)证明;取AB的中点G,连结B1G,
∵Al C1∥AC
又异面直线A1B与AC成60°角,
∴∠BAlCl=60°
在直三梭柱ABC-A1B1C1中,AB=BC=2,
∠ABC=90°
∴AlB=BC1,AlCl=![]()
∴AA1=2
∴四边形ABA1B1 为正方形
又E、G分别为BB1、AB的中点
∴AlE⊥BlG
又B1C1⊥平面ABB1A1,
∴B1C1⊥A1E
∵OG//BC,BC//B1C1
∴OG∥B1C1
∴O、G、B1、C1四点共面
 ∴AlE⊥平面GB1C1
∴AlE⊥平面GB1C1
∴AlE⊥OC1,
(Ⅲ)取A1C1的中点H,则
B1H⊥AlC1
∴BlH⊥平面CClA1。
过H作HM⊥A1C,连结BlM,则BlM⊥A1C,
∴∠B1MH为二面角B1―A1C―Cl的平面角.
在Rt△AlClC和Rt△AlMH中,AlH=![]() ,C1C=2,AlC=
,C1C=2,AlC=![]()
∴HM=![]()
又BlH=![]()
∴![]() B1MH=60°
B1MH=60°
∴二面角Bl-AlC―C1的大小为60°


科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是



查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆八中高三(下)第二次月考数学试卷(理科)(解析版) 题型:选择题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com