
| OA |
| OB |
| 1 |
| 3 |
| x2 | ||
|
| x2 | ||
|
|
|
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
|


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源:河北省衡水中学2011-2012学年高二上学期四调考试数学理科试题 题型:044
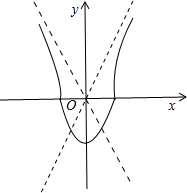
已知曲线C:4x2-y|y|=1
(Ⅰ)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(Ⅱ)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为坐标原点),求实数k的取值范围.
(其中O为坐标原点),求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:福建省福州三中2012届高三第四次月考数学理科试题 题型:044
已知曲线C:4x2+12xy+9y2-6x-3y=0在矩阵![]() 所对应的变换作用下得到曲线C1,求曲线C1的方程及焦点到准线的距离.
所对应的变换作用下得到曲线C1,求曲线C1的方程及焦点到准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(2)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为原点),求实数k的取值范围.
(其中O为原点),求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(2)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为原点),求实数k的取值范围.
(其中O为原点),求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com