
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了50名女性和50名男性,根据调研结果得到如图所示的等高条形图
(Ⅰ)完成下列2×2列联表:
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
(II)能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
【答案】解:(Ⅰ)根据等高条形图,计算女性不喜欢旅游的人数为50×0.3=15,
男性不喜欢旅游的人数为50×0.5=25,填写2×2列联表如下:
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | 35 | 15 | 50 |
男性 | 25 | 25 | 50 |
合计 | 60 | 40 | 100 |
(II)根据列联表中数据,计算
K2= ![]() =
= ![]() ≈4.167<5.024,
≈4.167<5.024,
对照临界值知,不能在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
【解析】(1)根据等高条形图,计算男、女性不喜欢旅游的人数,填写2×2列联表即可;
(2)根据列联表中数据,计算![]() ,对照临界值表得出结论。
,对照临界值表得出结论。
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.


科目:高中数学 来源: 题型:
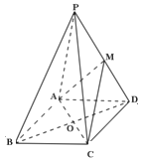
【题目】如图,已知在正四棱锥![]() 中,
中, ![]() 为侧棱
为侧棱![]() 的中点, 连接
的中点, 连接![]() 相交于点
相交于点![]() 。
。
(1)证明: ![]() ;
;
(2)证明: ![]() ;
;
(3)设![]() ,若质点从点
,若质点从点![]() 沿平面
沿平面![]() 与平面
与平面![]() 的表 面运动到点
的表 面运动到点![]() 的最短路径恰好经过点
的最短路径恰好经过点![]() ,求正四棱锥
,求正四棱锥 ![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
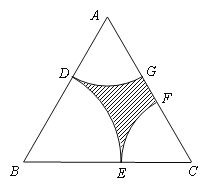
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布图中![]() 的值,并估计该企业的职工对该部门评分不低于80的概率;
的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率..
的概率..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求常数![]() 的值;
的值;
(2)设![]() ,证明函数
,证明函数![]() 在(1,+∞)上是减函数;
在(1,+∞)上是减函数;
(3)若函数![]() ,且
,且![]() 在区间[3,4]上没有零点,求实数
在区间[3,4]上没有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是A1B1上一点,若平面EBD与平面ABCD所成锐二面角的正切值为 ![]() ,设三棱锥A﹣A1D1E外接球的直径为a,则
,设三棱锥A﹣A1D1E外接球的直径为a,则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD的所有棱长均为6,点P在AC上,且AP=2PC,过P作四面体的截面,使截面平行于直线AB和CD,则该截面的周长为( )
A.16
B.12
C.10
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),a+b+c=0,且f(0)f(1)>0,设x1 , x2是方程f(x)=0的两个根,则|x1﹣x2|的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com