已知函数f(x)=ex,其图象在点P(2,f(2))处的切线为l.
(1)求y=f(x)、直线x=2及两坐标轴围成的图形绕x轴旋转一周所得几何体的体积;
(2)求y=f(x)、直线l及y轴围成图形的面积.
【答案】
分析:(1)本题要求的是一个旋转体的体积,看清组成图形的最主要的曲线,和组成图形的两个端点处的数据,用定积分写出体积的表示形式,得到结果.
(2)首先求出曲线在定点的切线,用上方的曲线的解析式减去下方曲线的解析式,把两个解析式做差以后,在0到2上积分,得到结果.
解答:解:(1)f(x)=e
x、直线x=2及两坐标轴围成的图形绕x轴旋转一周所得几何体的体积是
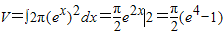
(2)函数f(x)=e
x,其图象在点P(2,f(2))处的切线为l.
直线l的斜率k=f'(2)=e
2,
则直线方程为:y=e
2x-e
2∴
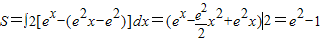 点评:
点评:本题考查用定积分求几何体的面积和体积,这是高中阶段所学的定积分的简单应用,解题时只要注意到体积和面积主要是由哪一条曲线构成就可以.

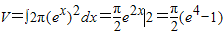
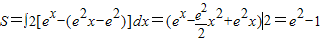


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案