
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)当线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距最小时,求直线
轴上的截距最小时,求直线![]() 的方程.
的方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】Fibonacci数列又称黄金分割数列,因为当n趋向于无穷大时,其相邻两项中的前项与后项的比值越来越接近黄金分割数![]() .已知Fibonacci数列的递推关系式为
.已知Fibonacci数列的递推关系式为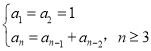 .
.
(1)证明:Fibonacci数列中任意相邻三项不可能成等比数列;
(2)Fibonacci数列{an}的偶数项依次构成一个新数列,记为{bn},证明:{bn+1-H2·bn}为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)若在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 是以
是以![]() 为顶点的等腰三角形,求直线
为顶点的等腰三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数![]() 的图象,只需把函数
的图象,只需把函数![]() ,
,![]() 的图象上所有的点( )
的图象上所有的点( )
A.向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.向右平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 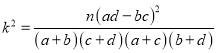 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
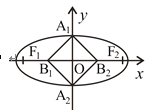
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com