
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数.当
上的偶函数.当![]() 时,
时, ![]() .
.
(1) 求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2) 若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据![]() 是偶函数,当
是偶函数,当![]() 时,
时, ![]() ,可得当
,可得当![]() 时,
时, ![]() ,
, ![]() ,求出
,求出![]() 可得切线斜率,求出
可得切线斜率,求出![]() ,可得切点坐标,由点斜式可得切线方程;(2)令
,可得切点坐标,由点斜式可得切线方程;(2)令![]() ,则原命题等价于
,则原命题等价于![]() ,
, ![]() 恒成立, 即
恒成立, 即![]() 恒成立,设
恒成立,设![]() ,利用导数研究函数的单调性,求出
,利用导数研究函数的单调性,求出![]() 的最大值为
的最大值为![]() ,从而可得实数
,从而可得实数![]() 的取值范围为
的取值范围为![]() .
.
试题解析:因为![]() 为偶函数,所以,
为偶函数,所以,
当![]() 时,则
时,则![]() ,故
,故 ![]() ,所以
,所以![]() ,
,
从而得到![]() ,
, ![]() ,
,
(1)当![]() 时,
时, ![]() ,所以
,所以![]()
所以在点![]() 的切线方程为:
的切线方程为: ![]() ,即
,即![]()
(2)关于![]() 的不等式
的不等式![]() 恒成立,即
恒成立,即 ![]() 恒成立
恒成立
令![]() ,则原命题等价于
,则原命题等价于![]() ,
, ![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
记![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 递增;当
递增;当![]() 时,
时, ![]() ,则
,则![]() 递减;
递减;
所以,当![]() 时,
时, ![]() 取极大值,也是最大值
取极大值,也是最大值![]() ,
,
所以![]() ,
,
即实数a的范围为![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与最值、不等式恒成立问题,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】若函数f(x)=sin2ax-![]() sin ax·cos ax-
sin ax·cos ax-![]() (a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为
(a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为![]() 的等差数列.
的等差数列.
(1)求a,b的值;
(2)若x0∈![]() ,且x0是y=f(x)的零点,试写出函数y=f(x)在
,且x0是y=f(x)的零点,试写出函数y=f(x)在![]() 上的单调增区间.
上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
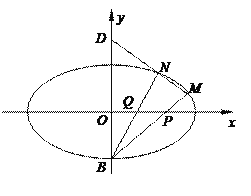
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的下顶点为
的下顶点为![]() ,点
,点![]() 是椭圆上异于点
是椭圆上异于点![]() 的动点,直线
的动点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.当点
的中点.当点![]() 运动到点
运动到点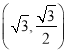 处时,点
处时,点![]() 的坐标为
的坐标为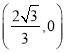 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 均在
均在![]() 轴右侧,且
轴右侧,且![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)≤0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,2017年双11全天交易额达到1682亿元,为规范和评估该行业的情况,相关管理部门制定出针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行评价,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成关于商品和服务评价的![]() 列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附:临界值表:

![]() 的观测值:
的观测值: 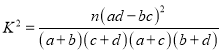 (其中
(其中![]() )
)
关于商品和服务评价的![]() 列联表:
列联表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com