
| A. | ③④ | B. | ②③ | C. | ①④ | D. | ①② |
分析 化简方程$\frac{x|x|}{16}+\frac{y|y|}{9}=-1$,从而作出函数y=f(x)的图象,
①由函数的图象判断函数的单调性;
②函数的零点可转化为方程的解,再转化为函数的图象的交点,从而判断零点;
③由函数的图象的变换可求其最值;
④由函数的图象的对称性可得方程为$\frac{y|y|}{16}+\frac{x|x|}{9}=1$,从而判断.
解答 解:①当x≥0且y≥0时,原方程化为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=-1,不成立;
当x<0且y<0时,原方程化为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1;
当x≥0且y<0时,原方程化为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=-1;
当x<0且y≥0时,原方程化为-$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=-1;
作出函数的图象如下,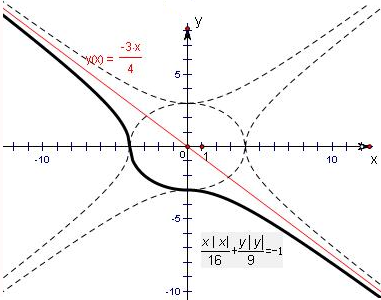
故①正确;
②由F(x)=4f(x)+3x=0得,f(x)=-$\frac{3}{4}$x;
由上图知方程无解,故②正确;
③根据①所作的图象可知,函数y=f(|x|)的最大值为-3,故错误;
④若函数g(x)和f(x)的图象关于原点对称,则用-x,-y分别代替x,y;
可得g(x)=-f(-x),则函数y=g(x)的图象是方程$\frac{x|x|}{16}+\frac{y|y|}{9}$=1确定的曲线,故不正确.
故选:D.
点评 本题考查了圆锥曲线的方程与其图象,同时考查了函数的图象及其变换,还考查了函数的图象与性质的应用,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (10,0) | B. | (0,4) | C. | (-6,-4) | D. | (6,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
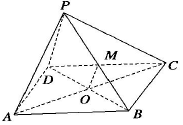 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com