
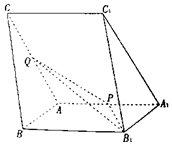
 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.分析 (1)取BC中点M,连接AM,则AM∥平面PQB1;
(2)作PN∥C1A1,则直线A1C1与平面PQB1所成角=直线PN与平面PQB1所成角,求出N到平面PQB1的距离,即可求直线A1C1与平面PQB1所成角的正弦值.
解答  解:(1)取BC中点M,连接AM,则AM∥平面PQB1;
解:(1)取BC中点M,连接AM,则AM∥平面PQB1;
(2)作QO⊥平面ABB1A1,与A1A延长线交于O,则AO=1,QO=$\sqrt{3}$,
OB1=$\sqrt{25+4-2×5×2×\frac{1}{2}}$=$\sqrt{19}$,∴QB1=$\sqrt{22}$,
∵B1P=2,PQ=2$\sqrt{3}$,
∴cos∠QPB1=$\frac{12+4-22}{2×2\sqrt{3}×2}$=-$\frac{\sqrt{3}}{6}$,
∴sin∠QPB1=$\frac{\sqrt{33}}{6}$,
∴${S}_{△PQ{B}_{1}}$=$\frac{1}{2}×2\sqrt{3}×2×\frac{\sqrt{33}}{6}$=$\sqrt{11}$,
作PN∥C1A1,则直线A1C1与平面PQB1所成角=直线PN与平面PQB1所成角,
∵${S}_{△PQN}=\frac{1}{2}×4×\sqrt{3}$=2$\sqrt{3}$,∴${V}_{{B}_{1}-PQN}$=$\frac{1}{3}×2\sqrt{3}×\sqrt{3}$=2,
设N到平面PQB1的距离为h,则$\frac{1}{3}×\sqrt{11}h=2$,∴h=$\frac{3}{\sqrt{11}}$,
∴直线A1C1与平面PQB1所成角的正弦值=$\frac{\frac{3}{\sqrt{11}}}{4}$=$\frac{3\sqrt{11}}{44}$.
点评 本题考查线面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.
某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{5}{4}$,1) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{4}{5}$,1) | D. | (-1,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com