
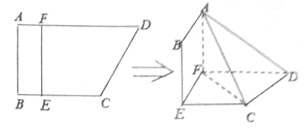
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)当![]() ,是否在折叠后的
,是否在折叠后的![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 点位置,若不存在,说明理由;
点位置,若不存在,说明理由;
(2)设![]() ,问当
,问当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积有最大值?并求出这个最大值.
的体积有最大值?并求出这个最大值.
【答案】(1)存在点![]() ,当
,当![]() 时使得
时使得![]() (2)当
(2)当![]() 时,体积最大值为
时,体积最大值为![]()
【解析】试题分析:(1)根据CP∥平面ABEF的性质,建立条件关系即可得到结论.(2)设BE=x,根据三棱锥的体积公式即可得到结论.
试题解析:
(1)若存在P,使得CP∥平面ABEF,此时λ=![]()
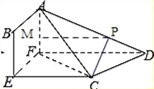
证明:当λ=![]() ,此时
,此时![]()
过P作MP∥FD,与AF交M,则![]()
又PD=5,故MP=3,
∵EC=3,MP∥FD∥EC,
∴MP∥EC,且MP=EC,故四边形MPCE为平行四边形,
∴PC∥ME,
∵CP平面ABEF,ME平面ABEF,
故答案为:CP∥平面ABEF成立。
(2)∵平面ABEF⊥平面EFDC,ABEF∩平面EFDC=EF,AF⊥EF,
∴AF⊥平面EFDC,
∵BE=x,∴AF=x,(0<x<4),FD=6x,
故三棱锥ACDF的体积![]()
![]() ,当
,当![]() 时,最大值为
时,最大值为![]()


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(Ⅰ)求应从水果类、点心类、小吃类中分别买回的种数;
(Ⅱ)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: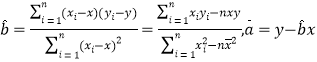 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴上,动点
轴上,动点![]() 满足
满足![]() ,且直线
,且直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点, ![]() 是线段
是线段![]() 的中点.
的中点.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是曲线
是曲线![]() 的焦点,过
的焦点,过![]() 的两条直线
的两条直线![]() ,
, ![]() 关于
关于![]() 轴对称,且
轴对称,且![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 、
、![]() 在第一象限,若四边形
在第一象限,若四边形![]() 的面积等于
的面积等于![]() ,求直线
,求直线![]() ,
, ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是矩形,
是矩形, ![]() ,
, ![]() 分别为边
分别为边![]() ,
, ![]() 的中点,
的中点, ![]() 与
与![]() 交于点
交于点![]() ,沿
,沿![]() 将矩形
将矩形![]() 折起,设
折起,设![]() ,
, ![]() ,二面角
,二面角![]() 的大小为
的大小为![]() .
.
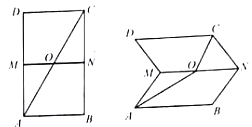
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)点![]() 时,点
时,点![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线L:kx-y+1+2k=0.
(1)求证:直线L过定点;
(2)若直线L交x轴负半轴于点A,交y正半轴于点B,△AOB的面积为S,试求S的最小值并求出此时直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)若数列{an}是的递增等差数列,其中的a3=5,且a1,a2,a5成等比数列,
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前项的和Tn.
,求数列{bn}的前项的和Tn.
(3)是否存在自然数m,使得![]() <Tn<
<Tn<![]() 对一切n∈N*恒成立?若存在,求出m的值;
对一切n∈N*恒成立?若存在,求出m的值;
若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个实数数列{an}满足条件: ![]() (d为常数,n∈N*),则称这一数列“伪等差数列”,d称为“伪公差”.给出下列关于某个伪等差数列{an}的结论:①对于任意的首项a1 , 若d<0,则这一数列必为有穷数列;②当d>0,a1>0时,这一数列必为单调递增数列;③这一数列可以是一个周期数列;④若这一数列的首项为1,伪公差为3,-
(d为常数,n∈N*),则称这一数列“伪等差数列”,d称为“伪公差”.给出下列关于某个伪等差数列{an}的结论:①对于任意的首项a1 , 若d<0,则这一数列必为有穷数列;②当d>0,a1>0时,这一数列必为单调递增数列;③这一数列可以是一个周期数列;④若这一数列的首项为1,伪公差为3,- ![]() 可以是这一数列中的一项;n∈N*⑤若这一数列的首项为0,第三项为﹣1,则这一数列的伪公差可以是
可以是这一数列中的一项;n∈N*⑤若这一数列的首项为0,第三项为﹣1,则这一数列的伪公差可以是 ![]() .其中正确的结论是 .
.其中正确的结论是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com