
����Ŀ���������̴�λ���㷨ͳ�ڡ��У���������һ��ҥ���������������裮��Զ��ΡΡ���߲㣬����㱶�ӱ����������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ���������˵����Զ����һ����ΰ�ķ��������Ϲ����������ƣ���һ���������һ�������2����ȫ������381յ�����ʶ����м�յ��?����ͬ�����Ȿ���л���һ���������⣺��һ����ͷһ��ɮ����ɮ������������Сɮ���˷�һ������С���и��������������ɰ��ģ�����˼�ǣ�����100�����з�100����ͷ����������һ�˷�3����С����3�˷�һ�������÷��꣮���ְ��շֲ�����İ취����100��������ѡȡ12����ȥ���õ�һ�����������ĵƣ���ôÿյ����Ҫ���ɵĴ�С��������Ϊ��A��1�ˣ�3�� ��B��2�ˣ�4�� ��C��3�ˣ�6�� ��D��3�ˣ�9��
���𰸡�A
���������ڵ�һ�������У�������ôӶ��㿪ʼÿһ��Ƶ��������һ������Ϊ2�ĵȱ�������Ϊ![]() ������ǰ7���
������ǰ7���![]() ���ɵȱ�����ǰ
���ɵȱ�����ǰ![]() ���ʽ���
���ʽ���![]() ��Ҳ����˵�����3յ�ƣ��ڵڶ��������У�100�������У�С���е�����ӦΪ����е�3��������ѡȡ��12����Ӧ�д����3����С����9�ˣ���������������貼�õ���յ�Ƶķ���Ӧ����ÿյ��������1����С����3�ˣ���ѡA��
��Ҳ����˵�����3յ�ƣ��ڵڶ��������У�100�������У�С���е�����ӦΪ����е�3��������ѡȡ��12����Ӧ�д����3����С����9�ˣ���������������貼�õ���յ�Ƶķ���Ӧ����ÿյ��������1����С����3�ˣ���ѡA��
��������ͼ��������Ҫ����ȱ����С��ֲ������֪ʶ��������������������Լ�ѧ������ѧ�Ļ����˽⣬���е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-5������ʽѡ��
��֪����ʽ![]()
![]() ������ʵ��
������ʵ��![]() �������
�������
������ʵ��![]() ����Сֵ
����Сֵ![]() ��
��
������![]() ��������
��������![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ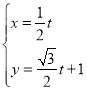 ��
��![]() ������������
Ϊ������������![]() ����ͨ����Ϊ
����ͨ����Ϊ![]() ��������ԭ��Ϊ���㣬
��������ԭ��Ϊ���㣬![]() ����������Ϊ���Ὠ��������ϵ��
����������Ϊ���Ὠ��������ϵ��
��I����ֱ��![]() �ļ����귽��������
�ļ����귽��������![]() �IJ������̣�
�IJ������̣�
��II�����D������![]() �ϣ�������
�ϣ�������![]() ����D����������ֱ��
����D����������ֱ��![]() ��ֱ����ȷ����D������.
��ֱ����ȷ����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������
������![]() ����������Ϊ
����������Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�����![]() ��
��![]() ���ϵ���ӰΪ��
���ϵ���ӰΪ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ��
�� ![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}ǰn���ΪSn �� an��0��n=1��2��������a1=a2=1���Ҷ�n��2�У�a1+a2+��+an��an=��a1+a2+��+an��1��an+1 �� ��S1S2+S2S3+S3S4+��+Sn��1Sn= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=kx+log9��9x+1����k��R����ż������
��1����k��ֵ��
��2��������g��x��=log9��a3x�� ![]() a����ͼ����f��x����ͼ������ֻ��һ�������㣬��a��ȡֵ��Χ��
a����ͼ����f��x����ͼ������ֻ��һ�������㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֢���DZ����ڸ���С���ϣ����ջ����ۣ��ر�Ӱ����˷�չ.ijУ��һ�����ʵ������С�飬�ڶԸ�Уѧ�����С��Ƿ�����������֢���ĵ����У����������110���ʾ�.���ջص�100����Ч�ʾ�����ͳ�ƣ��õ�����![]() ��������
��������

��1����Ů���Ƿ�����������֢���зֲ㣬�Ѿ���40��Ů���ʾ��г�ȡ��8���ʾ����ִ���8���ʾ����������ȡ3�ݣ�������������������֢���ʾ��ķ���Ϊ![]() �������������
�������������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��2�����ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ����������֢���Ա��йأ���ô�����ٽ�ֵ�����ȷ��
��ǰ������Ϊ����������֢���Ա��йأ���ô�����ٽ�ֵ�����ȷ��![]() ��ֵӦΪ���٣���˵������.���������Լ���ͳ����
��ֵӦΪ���٣���˵������.���������Լ���ͳ����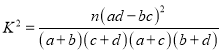 ������
������![]() .
.
�����Լ����ٽ�ֵ����
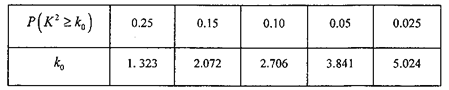
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ���ҹ���
���ҹ���![]() .
.

��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ��б�ʴ���0��ֱ��
��б�ʴ���0��ֱ��![]() ����Բ
����Բ![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
�� ![]() ��ֱ��
��ֱ��![]() ��
�� ![]() ��
��![]() ���ཻ��
���ཻ��![]() ��
�� ![]() ���㣬��
���㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1=1��an+1 ![]() =1����Sn=a12+a22+��+an2 �� ��S2n+1��Sn��
=1����Sn=a12+a22+��+an2 �� ��S2n+1��Sn�� ![]() ������n��N*���������������m����Сֵ�� ��
������n��N*���������������m����Сֵ�� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com