
【题目】将函数![]() 的图象上所有点的纵坐标不变,横坐标变为原来的
的图象上所有点的纵坐标不变,横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位,若得到的图象关于原点对称,则当
个单位,若得到的图象关于原点对称,则当![]() 时,
时,![]() 的值域为( )
的值域为( )
A.![]() B.
B.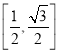 C.
C.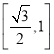 D.
D.![]()
科目:高中数学 来源: 题型:
【题目】台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD,在点E,F处各放一个目标球,表演者先将母球放在点A处,通过击打母球,使其依次撞击点E,F处的目标球,最后停在点C处,若AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,则该正方形的边长为( )
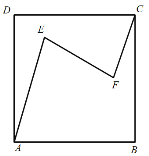
A.50![]() cmB.40
cmB.40![]() cmC.50cmD.20
cmC.50cmD.20![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,
,![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() ,
,![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() ,以
,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,如图所示,山区边界曲线为
,如图所示,山区边界曲线为![]() :
:![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
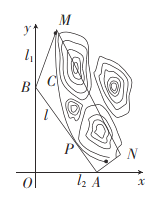
(1)设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,若公路
两点,若公路![]() 的斜率为-1,求
的斜率为-1,求![]() 的长;
的长;
(2)在(1)条件下,测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.直线
轴正半轴为极轴建立极坐标系.直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为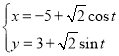 (
(![]() 是参数)以原点
是参数)以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和的直线
的普通方程和的直线![]() 直角坐标方程;
直角坐标方程;
(2)设直线![]() 与
与![]() 轴交点分别是
轴交点分别是![]() ,点
,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会(以下简称武汉军运会)专题新闻发布会在武汉举行,武汉军运会会徽、吉祥物正式公布.武汉军运会将于![]() 年
年![]() 月
月![]() 日举行,赛期
日举行,赛期![]() 天.若将
天.若将![]() 名志愿者分配到两个运动场馆进行服务,每个运动场馆至少
名志愿者分配到两个运动场馆进行服务,每个运动场馆至少![]() 名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com