
ΓΨΧβΡΩΓΩΈΣΆΤ––ΓΑ–¬ΩΈΧΟΓ±ΫΧ―ßΖ®Θ§Ρ≥Μ·―ßάœ ΠΖ÷±π”Ο¥ΪΆ≥ΫΧ―ßΚΆΓΑ–¬ΩΈΧΟΓ±ΝΫ÷÷≤ΜΆ§ΒΡΫΧ―ßΖΫ ΫΘ§‘ΎΦΉΓΔ““ΝΫΗωΤΫ––ΑύΫχ––ΫΧ―ß Β―ιΘ§ΈΣΝΥΫβΫΧ―ß–ßΙϊΘ§ΤΎ÷–ΩΦ ‘ΚσΘ§Ζ÷±π¥”ΝΫΗωΑύΦΕ÷–ΗςΥφΜζ≥ι»Γ![]() Οϊ―ß…ζΒΡ≥…Φ®Ϋχ––Ά≥ΦΤΘ§Ής≥ωΒΡΨΞ“ΕΆΦ»γœ¬ΆΦΘ§Φ«≥…Φ®≤ΜΒΆ”Ύ
Οϊ―ß…ζΒΡ≥…Φ®Ϋχ––Ά≥ΦΤΘ§Ής≥ωΒΡΨΞ“ΕΆΦ»γœ¬ΆΦΘ§Φ«≥…Φ®≤ΜΒΆ”Ύ![]() Ζ÷’ΏΈΣΓΑ≥…Φ®”≈ΝΦΓ±.
Ζ÷’ΏΈΣΓΑ≥…Φ®”≈ΝΦΓ±.
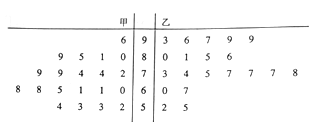
Θ®1Θ©Ζ÷±πΦΤΥψΦΉΓΔ““ΝΫΑύ![]() Ηω―υ±Ψ÷–Θ§Μ·―ßΖ÷ ΐ«Α °ΒΡΤΫΨυΖ÷Θ§≤ΔΨί¥Υ≈–ΕœΡΡ÷÷ΫΧ―ßΖΫ ΫΒΡΫΧ―ß–ßΙϊΗϋ
Ηω―υ±Ψ÷–Θ§Μ·―ßΖ÷ ΐ«Α °ΒΡΤΫΨυΖ÷Θ§≤ΔΨί¥Υ≈–ΕœΡΡ÷÷ΫΧ―ßΖΫ ΫΒΡΫΧ―ß–ßΙϊΗϋ
Φ―ΘΜ
Θ®2Θ©ΦΉΓΔ““ΝΫΑύ![]() Ηω―υ±Ψ÷–Θ§≥…Φ®‘Ύ
Ηω―υ±Ψ÷–Θ§≥…Φ®‘Ύ![]() Ζ÷“‘œ¬Θ®≤ΜΚ§
Ζ÷“‘œ¬Θ®≤ΜΚ§![]() Ζ÷Θ©ΒΡ―ß…ζ÷–»Έ“β―Γ»Γ
Ζ÷Θ©ΒΡ―ß…ζ÷–»Έ“β―Γ»Γ![]() »ΥΘ§«σ’β
»ΥΘ§«σ’β![]() »Υά¥Ή‘≤ΜΆ§ΑύΦΕΒΡΗ≈¬ ΘΜ
»Υά¥Ή‘≤ΜΆ§ΑύΦΕΒΡΗ≈¬ ΘΜ
Θ®3Θ©”…“‘…œΆ≥ΦΤ ΐΨίΧν–¥œ¬Οφ![]() Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ
Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣΓΑ≥…Φ®”≈ΝΦ”κΫΧ―ßΖΫ Ϋ”–ΙΊΓ±?
ΒΡ«ΑΧαœ¬»œΈΣΓΑ≥…Φ®”≈ΝΦ”κΫΧ―ßΖΫ Ϋ”–ΙΊΓ±?
ΦΉΑύ | ““Αύ | ΉήΦΤ | |
≥…Φ®”≈ΝΦ | |||
≥…Φ®≤Μ”≈ΝΦ | |||
ΉήΦΤ |
ΗΫΘΚ 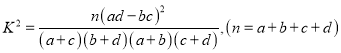
ΕάΝΔ–‘Φλ―ιΝΌΫγ÷Β±μΘΚ
|
|
|
|
|
|
|
|
|
|
ΓΨ¥πΑΗΓΩΘ®1Θ©ΗΏ–ßΩΈΧΟΗϋΦ―ΘΜΘ®2Θ© ![]() ΘΜΘ®3Θ©Ρή.
ΘΜΘ®3Θ©Ρή.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…Χβ“βΘ§Ω…ΗυΨίΨΞ“ΕΆΦΥυΧαΙ© ΐΨίΘ§Ε‘ΦΉ““ΝΫΗωΑύΗς»Γ«Α10ΟϊΒΡΖ÷ ΐΘ§≤ΔΦΤΥψΤδΤΫΨυ÷ΒΦ¥Ω…Θ§”…¥ΥΩ…≈–ΕœΗΏ–ßΩΈΧΟΗϋΦ―ΘΜΘ®2Θ©”…ΨΞ“ΕΆΦΆ≥ΦΤΝΫΗωΑύ60Ζ÷“‘œ¬ΒΡ»Υ ΐΘ§‘ΌΑ¥Ι≈ΒδΗ≈–ΆΗ≈¬ ΒΡΦΤΥψΙΪ ΫΫχ––‘ΥΥψΦ¥Ω…ΘΜΘ®3Θ©ΗυΨίΧβ“βΘ§”…ΨΞ“ΕΆΦΆ≥ΦΤΝ–ΝΣ±μ÷–ΒΡ»Υ ΐΘ§ΗυΨίΙΪ ΫΥψ≥ω![]() Θ§‘Ό±»Ε‘ΝΌΫγ÷Β±μΘ§¥”ΕχΩ…ΒΟ≥ωΫα¬έ.
Θ§‘Ό±»Ε‘ΝΌΫγ÷Β±μΘ§¥”ΕχΩ…ΒΟ≥ωΫα¬έ.
‘ΧβΫβΈωΘΚΘ®1Θ©ΦΉΑύ―υ±ΨΜ·―ß≥…Φ®«Α °ΒΡΤΫΨυΖ÷ΈΣ
![]() ΘΜ
ΘΜ
““Αύ―υ±ΨΜ·―ß≥…Φ®«Α °ΒΡΤΫΨυΖ÷ΈΣ
![]() ΘΜ
ΘΜ
ΦΉΑύ―υ±ΨΜ·―ß≥…Φ®«Α °ΒΡΤΫΨυΖ÷‘ΕΒΆ”Ύ““Αύ―υ±ΨΜ·―ß≥…Φ®«Α °ΒΡΤΫΨυΖ÷Θ§¥σ÷¬Ω…“‘≈–ΕœΓΑΗΏ–ßΩΈΧΟΓ±ΫΧ―ßΖΫ ΫΒΡΫΧ―ß–ßΙϊΗϋΦ―.
Θ®2Θ©―υ±Ψ÷–≥…Φ®![]() Ζ÷“‘œ¬ΒΡ―ß…ζ÷–ΦΉΑύ”–
Ζ÷“‘œ¬ΒΡ―ß…ζ÷–ΦΉΑύ”–![]() »ΥΘ§Φ«ΈΣΘΚ
»ΥΘ§Φ«ΈΣΘΚ ![]() Θ§““Αύ”–
Θ§““Αύ”–![]() »ΥΘ§Φ«ΈΣΘΚ
»ΥΘ§Φ«ΈΣΘΚ ![]() .
.
‘ρ¥”![]() Θ§
Θ§ ![]() ΝυΗω‘ΣΥΊ÷–»Έ“β―Γ
ΝυΗω‘ΣΥΊ÷–»Έ“β―Γ![]() ΗωΒΡΥυ”–Μυ±Ψ ¬Φΰ»γœ¬ΘΚ
ΗωΒΡΥυ”–Μυ±Ψ ¬Φΰ»γœ¬ΘΚ
![]() Θ§“ΜΙ≤”–
Θ§“ΜΙ≤”–![]() ΗωΜυ±Ψ ¬ΦΰΘ§
ΗωΜυ±Ψ ¬ΦΰΘ§
…η![]() ±μ ΨΓΑ’β
±μ ΨΓΑ’β![]() »Υά¥Ή‘≤ΜΆ§ΑύΦΕΓ±”–»γœ¬ΘΚ
»Υά¥Ή‘≤ΜΆ§ΑύΦΕΓ±”–»γœ¬ΘΚ
![]() Θ§“ΜΙ≤”–
Θ§“ΜΙ≤”–![]() ΗωΜυ±Ψ ¬ΦΰΘ§
ΗωΜυ±Ψ ¬ΦΰΘ§
Υυ“‘![]() .
.
Θ®3Θ©
ΦΉΑύ | ““Αύ | ΉήΦΤ | |
≥…Φ®”≈ΝΦ |
|
|
|
≥…Φ®≤Μ”≈ΝΦ |
|
|
|
ΉήΦΤ |
|
|
|
ΗυΨί![]() Ν–ΝΣ±μ÷–ΒΡ ΐΨίΘ§ΒΟ
Ν–ΝΣ±μ÷–ΒΡ ΐΨίΘ§ΒΟ![]() ΒΡΙέ≤β÷ΒΈΣ
ΒΡΙέ≤β÷ΒΈΣ
![]() Θ§
Θ§
ΓύΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣΓΑ≥…Φ®”≈ΝΦ”κΫΧ―ßΖΫ Ϋ”–ΙΊΓ±.
ΒΡ«ΑΧαœ¬»œΈΣΓΑ≥…Φ®”≈ΝΦ”κΫΧ―ßΖΫ Ϋ”–ΙΊΓ±.


 ΤΏ–«ΆΦ ιΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΤΏ–«ΆΦ ιΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ ≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ
≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©=![]() Θ§gΘ®xΘ©=aΘ®x+bΘ©Θ®0ΘΦaΓή1Θ§bΓή0Θ©Θ°
Θ§gΘ®xΘ©=aΘ®x+bΘ©Θ®0ΘΦaΓή1Θ§bΓή0Θ©Θ°
Θ®1Θ©Χ÷¬έΚ· ΐy=fΘ®xΘ©gΘ®xΘ©ΒΡΤφ≈Φ–‘ΘΜ
Θ®2Θ©Β±b=0 ±Θ§≈–ΕœΚ· ΐy=![]() ‘ΎΘ®©¹1Θ§1Θ©…œΒΡΒΞΒς–‘Θ§≤ΔΥΒΟςάμ”…ΘΜ
‘ΎΘ®©¹1Θ§1Θ©…œΒΡΒΞΒς–‘Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©…ηhΘ®xΘ©=|af2Θ®xΘ©©¹![]() |Θ§»τhΘ®xΘ©ΒΡΉν¥σ÷ΒΈΣ2Θ§«σa+bΒΡ»Γ÷ΒΖΕΈßΘ°
|Θ§»τhΘ®xΘ©ΒΡΉν¥σ÷ΒΈΣ2Θ§«σa+bΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .»τ
.»τ![]() ±ΖΫ≥Χ
±ΖΫ≥Χ![]() ”–ΝΫ Ηω≤ΜΆ§ΒΡ ΒΗυΘ§‘ρ Β ΐ
”–ΝΫ Ηω≤ΜΆ§ΒΡ ΒΗυΘ§‘ρ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß «________ΘΜ»τ
ΒΡ»Γ÷ΒΖΕΈß «________ΘΜ»τ![]() ΒΡ÷Β”ρΈΣ
ΒΡ÷Β”ρΈΣ![]() Θ§‘ρ Β ΐ
Θ§‘ρ Β ΐ![]() ΒΡ
ΒΡ
»Γ÷ΒΖΕΈß «________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΫΙΒψ‘Ύ![]() ÷α…œΒΡΆ÷‘≤
÷α…œΒΡΆ÷‘≤![]() ΒΡ÷––Ρ «‘≠Βψ
ΒΡ÷––Ρ «‘≠Βψ![]() Θ§άκ–Ρ¬ ΈΣΥΪ«ζœΏ
Θ§άκ–Ρ¬ ΈΣΥΪ«ζœΏ![]() άκ–Ρ¬ ΒΡ“ΜΑκΘ§÷±œΏ
άκ–Ρ¬ ΒΡ“ΜΑκΘ§÷±œΏ![]() ±ΜΆ÷‘≤
±ΜΆ÷‘≤![]() ΫΊΒΟΒΡœΏΕΈ≥ΛΈΣ
ΫΊΒΟΒΡœΏΕΈ≥ΛΈΣ![]() .÷±œΏ
.÷±œΏ![]() ΘΚ
ΘΚ ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§”κΆ÷‘≤
Θ§”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΗωœύ“λΒψΘ§«“
ΝΫΗωœύ“λΒψΘ§«“![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐ![]() Θ§ Ι
Θ§ Ι![]() ΘΩ»τ¥φ‘ΎΘ§«σ
ΘΩ»τ¥φ‘ΎΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΟϋΧβ’ΐ»ΖΒΡ «__________Θ°Θ®–¥≥ωΥυ”–’ΐ»ΖΟϋΧβΒΡ–ρΚ≈Θ©
ΔΌ“―÷Σ![]() Θ§ΓΑ
Θ§ΓΑ![]() «“
«“![]() Γ± «ΓΑ
Γ± «ΓΑ![]() Γ±ΒΡ≥δ“ΣΧθΦΰΘΜ
Γ±ΒΡ≥δ“ΣΧθΦΰΘΜ
ΔΎ“―÷ΣΤΫΟφœρΝΩ![]() Θ§ΓΑ
Θ§ΓΑ![]() «“
«“![]() Γ± «ΓΑ
Γ± «ΓΑ![]() Γ±ΒΡ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰΘΜ
Γ±ΒΡ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰΘΜ
Δέ“―÷Σ![]() Θ§ΓΑ
Θ§ΓΑ![]() Γ± «ΓΑ
Γ± «ΓΑ![]() Γ±ΒΡ≥δΖ÷≤Μ±Ί“ΣΧθΦΰΘΜ
Γ±ΒΡ≥δΖ÷≤Μ±Ί“ΣΧθΦΰΘΜ
ΔήΟϋΧβ![]() ΘΚΓΑ
ΘΚΓΑ![]() Θ§ Ι
Θ§ Ι![]() «“
«“![]() Γ±ΒΡΖώΕ®ΈΣ
Γ±ΒΡΖώΕ®ΈΣ![]() ΘΚΓΑ
ΘΚΓΑ![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() «“
«“![]() Γ±
Γ±
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷Σ«ζœΏ
÷–Θ§“―÷Σ«ζœΏ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§‘Ύ“‘
ΈΣ≤Έ ΐΘ©Θ§‘Ύ“‘![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ
÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ”κ
”κ![]() ΒΡΫΜΒψ
ΒΡΫΜΒψ![]() ΒΡ÷±Ϋ«Ήχ±ξΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΘΜ
Θ®2Θ©…ηΒψ![]() Θ§
Θ§ ![]() Ζ÷±πΈΣ«ζœΏ
Ζ÷±πΈΣ«ζœΏ![]() …œΒΡΕ·ΒψΘ§«σ
…œΒΡΕ·ΒψΘ§«σ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©»τ![]() ‘ΎΕ®“ε”ρ…œΈΣΒΞΒςΒίΦθΚ· ΐΘ§«σ Β ΐ
‘ΎΕ®“ε”ρ…œΈΣΒΞΒςΒίΦθΚ· ΐΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Κψ≥…ΝΔ«“
Κψ≥…ΝΔ«“![]() ”–Έ®“ΜΝψΒψΘ§»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψ
”–Έ®“ΜΝψΒψΘ§»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψ![]() Θ§
Θ§ ![]() ΒΡ
ΒΡ![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ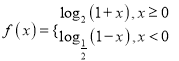 .
.
Θ®1Θ©≈–ΕœΚ· ΐ![]() ΒΡΤφ≈Φ–‘ΘΜ
ΒΡΤφ≈Φ–‘ΘΜ
Θ®2Θ©Ε‘»Έ“βΝΫΗω Β ΐ![]() Θ§«σ÷ΛΘΚΒ±
Θ§«σ÷ΛΘΚΒ±![]() ±Θ§
±Θ§ ![]() ΘΜ
ΘΜ
Θ®3Θ©Ε‘»ΈΚΈ Β ΐ![]() Θ§
Θ§ ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®ΔώΘ©«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®ΔρΘ©«σ÷ΛΘΚΒ±![]() ±Θ§
±Θ§ ![]() ΘΜ
ΘΜ
Θ®ΔσΘ©»τ![]() Ε‘»Έ“β
Ε‘»Έ“β![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com