
【题目】已知函数![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)通过讨论a的范围,结合函数的单调性求出函数的最小值,从而确定a的范围即可.
解:(Ⅰ)函数f(x)的定义域为![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,f(x)在
,f(x)在![]() 上为增函数.
上为增函数.
②当a>0时,由![]() 得
得![]() ;
;
由![]() 得
得![]() ,
,
所以f(x)在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
综上所述,①当![]() 时,函数f(x)在
时,函数f(x)在![]() 上为增函数
上为增函数
②当a>0时,f(x)在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
(Ⅱ)①当a=0时,因为![]() ,所以
,所以![]() 恒成立,所以a=0符合题意.
恒成立,所以a=0符合题意.
②当a<0时,![]() ,因为
,因为![]() ,所以
,所以![]() 不恒成立,舍去.
不恒成立,舍去.
③当a>0时,由(Ⅰ)知f(x)在![]() 上为减函数,f(x)在
上为减函数,f(x)在![]() 上为增函数.
上为增函数.
下面先证明:![]() .
.
设![]() ,因为
,因为![]() ,
,
所以p(a)在![]() 上为增函数.
上为增函数.
所以![]() ,因此有
,因此有![]() .
.
所以f(x)在![]() 上为增函数.
上为增函数.
所以![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
由![]() 得
得![]() ;由
;由![]() 得
得![]() .
.
所以![]() 在
在![]() 上为减函数,
上为减函数,![]() 在
在![]() 上为增函数.
上为增函数.
所以![]() .
.
所以q(a)在![]() 上为增函数,
上为增函数,
所以![]() .所以
.所以![]() .
.
所以![]() 恒成立.
恒成立.
故a>0符合题意.
综上可知,a的取值范围是![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某学校开设了射击选修课,规定向![]() 、
、![]() 两个靶进行射击:先向
两个靶进行射击:先向![]() 靶射击一次,命中得1分,没有命中得0分,向
靶射击一次,命中得1分,没有命中得0分,向![]() 靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向
靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,向
,向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
(1)求小明同学恰好命中一次的概率;
(2)求小明同学获得总分![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠病毒肺炎(COVID﹣19)疫情在武汉爆发,并以极快的速度在全国传播开来.因该病毒暂无临床特效药可用,因此防控难度极大.湖北某地防疫防控部门决定进行全面入户排查4类人员:新冠患者、疑似患者、普通感冒发热者和新冠密切接触者,过程中排查到一户5口之家被确认为新冠肺炎密切接触者,按要求进一步对该5名成员逐一进行核糖核酸检测,若出现阳性,则该家庭定义为“感染高危户”,设该家庭每个成员检测呈阳性的概率相同均为![]() ,且相互独立,该家庭至少检测了4人才能确定为“感染高危户”的概率为
,且相互独立,该家庭至少检测了4人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,此时
最大,此时![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱长为4,过点
的底面边长为2,侧棱长为4,过点![]() 作平面
作平面![]() 与正四棱柱的三条侧棱
与正四棱柱的三条侧棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,且
,且![]() ,若多面体
,若多面体![]() 和多面体
和多面体![]() 的体积比为3∶5,则截面
的体积比为3∶5,则截面![]() 的周长为_________.
的周长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
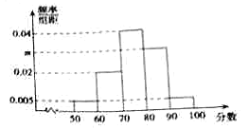
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() 的动点,设直线
的动点,设直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)当椭圆![]() 内切于圆
内切于圆![]() 时,设动直线
时,设动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,问:
,问:![]() 的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com