
����Ŀ��������ԲC�� ![]() =1��a��b��0������Բ����ԭ��O���뾶Ϊ
=1��a��b��0������Բ����ԭ��O���뾶Ϊ ![]() ��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF��
��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF�� ![]() ��0����������ϵ�һ���˵㵽F�ľ���Ϊ
��0����������ϵ�һ���˵㵽F�ľ���Ϊ ![]() ��
��
��������ԲC�ķ��̺��䡰Բ�����̣�
����P����ԲC�ġ�Բ���ϵĶ��㣬����P����Բ������l1 �� l2����Բ���ڵ�M��N��
����������PΪ��Բ����y��������Ľ���ʱ����ֱ��l1 �� l2�ķ��̲�֤��l1��l2��
��������֤���߶�MN�ij�Ϊ��ֵ��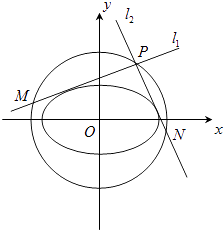
���𰸡����⣺����ԲC��һ������ΪF�� ![]() ��0����������ϵ�һ���˵㵽F�ľ���Ϊ
��0����������ϵ�һ���˵㵽F�ľ���Ϊ ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() =1��
=1��
����Բ����Ϊ ![]() ��
��
��Բ����Ϊx2+y2=4��
����֤������������Բx2+y2=4��y��������Ľ���ΪP��0��2����
�����P��0��2��������Բ���е�ֱ��Ϊy=kx+2��
����  �ã�1+3k2��x2+12kx+9=0��
�ã�1+3k2��x2+12kx+9=0��
��ֱ��y=kx+2����Բ���У�
���=144k2��4��9��1+3k2��=0�����k=��1��
��l1��l2����Ϊy=x+2��y=��x+2��
�� ![]() ��
��
��l1��l2��
�������ٵ�ֱ��l1��l2����һ��б�ʲ�����ʱ��������ֱ��l1б�ʲ����ڣ�
��l1�� ![]() ��
��
��l1�� ![]() ʱ��l1��Բ���ڵ�
ʱ��l1��Բ���ڵ� ![]() ��
��
��ʱl2Ϊy=1����y=��1������Ȼֱ��l1��l2��ֱ��
ͬ����֤��l1�� ![]() ʱ��ֱ��l1��l2��ֱ��
ʱ��ֱ��l1��l2��ֱ��
�ڵ�l1��l2б�ʴ���ʱ�����P��x0��y0�������� ![]() ��
��
�辭����P��x0��y0������Բ���е�ֱ��Ϊy=t��x��x0��+y0��
���� 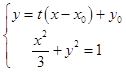
�� ![]() ��
��
�ɡ�=0���������� ![]() ��
��
�� ![]() ������
������ ![]() ��
��
��l1��l2��б�ʷֱ�Ϊt1��t2��
��l1��l2����Բ���У�
��t1��t2������������ ![]() ��
��
��t1t2=��1����l1��l2��ֱ��
�ۺϢ٢�֪����l1��l2������P��x0��y0�����ֱַ���Բ�ڵ�M��N����l1��l2��ֱ��
���߶�MNΪԲx2+y2=4��ֱ����|MN|=4�� ���߶�MN�ij�Ϊ��ֵ��
������������������֪��Բ�ı����̼��� ![]() ���ɵó�������i����ֱ�߷��̴�����Բ����ת��Ϊ����x��һԪ���η��̣�����ֱ������Բ������=0�����ɽ��k��ֵ���������ô�ֱ��б�ʵĹ�ϵ����֤������ii���������ۣ�l1��l2������P��x0��y0�����ֱַ���Բ�ڵ�M��N����������ֱ���е�б���Ƿ���ڣ�����l1��l2��ֱ�����ɵó��߶�MNΪԲx2+y2=4��ֱ����
���ɵó�������i����ֱ�߷��̴�����Բ����ת��Ϊ����x��һԪ���η��̣�����ֱ������Բ������=0�����ɽ��k��ֵ���������ô�ֱ��б�ʵĹ�ϵ����֤������ii���������ۣ�l1��l2������P��x0��y0�����ֱַ���Բ�ڵ�M��N����������ֱ���е�б���Ƿ���ڣ�����l1��l2��ֱ�����ɵó��߶�MNΪԲx2+y2=4��ֱ����


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2���������Ρ�ABC�У�DΪBC���е㣬E��F�ֱ��ڱ�CA��AB�ϣ� 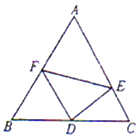
��1���� ![]() ����CE�ij���
����CE�ij���
��2������EDF=60�㣬�ʣ�����CDEȡ��ֵʱ����DEF�������С��������������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��FΪ�����������C��y2=2px��p��0���ϵ�����A��B���� ![]() =3
=3 ![]() ������AB���е㵽�ߵľ���Ϊ
������AB���е㵽�ߵľ���Ϊ ![]() ���������ߵķ���Ϊ ��
���������ߵķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC1��x2+y2=r2��r��0����ֱ��l0��y= ![]() ���У���AΪԲC1��һ���㣬AN��x���ڵ�N���Ҷ���M����
���У���AΪԲC1��һ���㣬AN��x���ڵ�N���Ҷ���M���� ![]() ���趯��M�Ĺ켣Ϊ����C��
���趯��M�Ĺ켣Ϊ����C��
��1����M�Ĺ켣����C�ķ��̣�
��2����ֱ��l������C�ཻ�ڲ�ͬ������P��Q��������PQΪֱ����Բ������ԭ��O�����߶�PQ���ȵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��
�� ![]() �����������x1 �� x2��[1��2]����x1��x2ʱ��[|f��x1��|��|f��x2��|]��x1��x2����0����ʵ��a��ȡֵ��ΧΪ�� ��
�����������x1 �� x2��[1��2]����x1��x2ʱ��[|f��x1��|��|f��x2��|]��x1��x2����0����ʵ��a��ȡֵ��ΧΪ�� ��
A.[�� ![]() ��
�� ![]() ]
]
B.[�� ![]() ��
�� ![]() ]
]
C.[�� ![]() ��
�� ![]() ]
]
D.[��e2 �� e2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ϊ ![]() ��������A��BCD��ÿ�����㶼�ڰ뾶ΪR����O�������ϣ�����O�ڴ������ڲ�����R��BC=2��3����EΪ�߶�BD��һ�㣬��DE=2EB������E����O�Ľ��棬�����ý���Բ�����ȡֵ��Χ�ǣ� ��
��������A��BCD��ÿ�����㶼�ڰ뾶ΪR����O�������ϣ�����O�ڴ������ڲ�����R��BC=2��3����EΪ�߶�BD��һ�㣬��DE=2EB������E����O�Ľ��棬�����ý���Բ�����ȡֵ��Χ�ǣ� �� 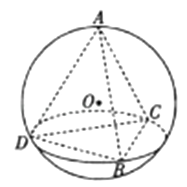
A.[4��12��]
B.[8��16��]
C.[8��12��]
D.[12��16��]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-4�����������뼫����ϵ]
��֪����C1�IJ�������Ϊ ![]() ��tΪ����������ԭ��OΪ���㣬��x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ
��tΪ����������ԭ��OΪ���㣬��x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ ![]() ��
��
����������C2��ֱ������ϵ���̣�
������M1������C1�ϵĵ㣬M2������C2�ϵĵ㣬��|M1M2|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��ԲO�����ڵ�B��CDΪԲO�����㣬�ӳ�AD��ԲO�ڵ�E��BF��CD�ҽ�ED�ڵ�F
����֤������BCE�ס�FDB��
������BEΪԲO��ֱ������EBF=��CBD��BF=2����ADED��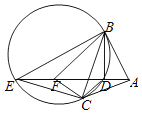
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-4������ϵ���������]����ƽ����ȡ��һ��������ϵ���Լ�����Ϊֱ������ϵ��x��������ᣬ�Ԧ�= ![]() ��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ�������
��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ������� ![]() ��tΪ��������
��t��������
��1��д��ֱ��l����ͨ����������C�ļ����귽�̣�
��2����ƽ���������任���������ʽΪ ![]() ����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com