
设a为实数,记函数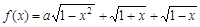 的最大值为
的最大值为 .
.
(1)设t=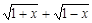 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;
(2)求 ;
;
(3)试求满足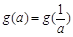 的所有实数a.
的所有实数a.
(1)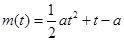 ,
, ;(2)
;(2) =
=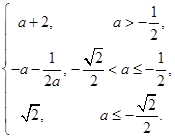 (3)
(3) .
.
解析试题分析:(1)根据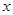 的取值范围求出
的取值范围求出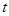 的范围,再将
的范围,再将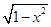 用含
用含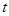 的式子表示;(2)由题意知
的式子表示;(2)由题意知 即为函数
即为函数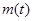
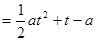 ,
,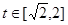 的最大值,因为对称轴含有参数
的最大值,因为对称轴含有参数 ,所以要讨论处理;(3)根据(2)问得出的
,所以要讨论处理;(3)根据(2)问得出的 ,由
,由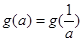 在对应区域上讨论解答即可.
在对应区域上讨论解答即可.
试题解析:(1)∵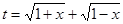 ,∴要使
,∴要使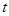 有意义,必须
有意义,必须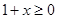 且
且 ,即
,即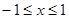 .
.
∵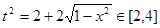 ,且
,且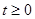 ①
①
∴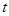 的取值范围是
的取值范围是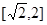 , 2分
, 2分
由①得: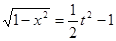 ,
,
∴
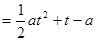 ,
,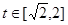 . 4分
. 4分
(2)由题意知 即为函数
即为函数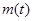
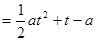 ,
,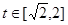 的最大值,
的最大值,
∵直线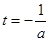 是抛物线
是抛物线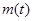
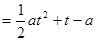 的对称轴, 5分
的对称轴, 5分
∴可分以下几种情况进行讨论:
①当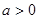 时,函数
时,函数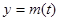 ,
,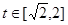 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由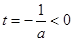 知
知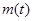 在
在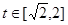 上单调递增,故
上单调递增,故

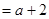 ;
;
②当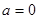 时,
时,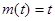 ,
,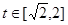 ,有
,有 =2;
=2;
③当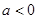 时,,函数
时,,函数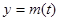 ,
,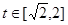 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若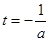
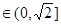 即
即 时,
时,
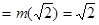 ,
,
若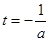
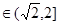 即
即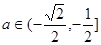 时,
时,
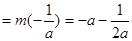 ,
,
若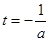
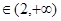 即
即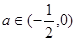 时,
时,

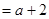 . 9分
. 9分
综上所述,有 =
=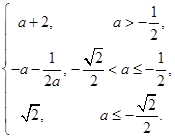 10分
10分
(3)当 时,
时,
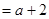
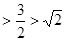 ;
;
当


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值);
(Ⅲ)使用若干年后,对机床的处理方案有两种:
(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(2)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在半径为 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在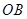 上,设矩形
上,设矩形 的面积为
的面积为 ,
,
(Ⅰ)按下列要求求出函数关系式:
①设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
(Ⅱ)请你选用(1)中的一个函数关系式,求出 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某公司生产品牌服装的年固定成本是10万元,每生产千件,须另投入2 7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且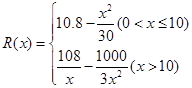
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?(注:年利润=年销售收入 年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求,使价格连续下跌.现有三种价格模拟函数:①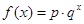 ;②
;②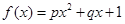 ;③
;③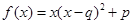 .(以上三式中
.(以上三式中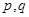 均为常数,且
均为常数,且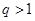 )
)
(1)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(2)若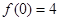 ,
,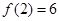 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是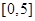 .其中
.其中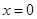 表示8月1日,
表示8月1日,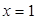 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(3)在(2)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金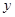 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:①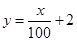 ;②
;②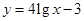 .
.
试分析这两个函数模型是否符合公司要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com