
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若不等式![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,证明:
时,证明:![]()
![]() .
.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:(1)求出![]() 的导函数
的导函数![]() ,由
,由![]() 得增区间,由
得增区间,由![]() 得减区间,注意在解不等式时要按
得减区间,注意在解不等式时要按![]() 的值分类讨论;
的值分类讨论;
(2)由(1)的结论知当![]() 时,
时,![]() ,题中不等式成立,而当
,题中不等式成立,而当![]() 时,题中不等式不恒成立;
时,题中不等式不恒成立;
(3)![]() 时,由(2)知
时,由(2)知![]() 上有
上有![]() ,从而
,从而![]() ,令
,令![]() ,然后所有不等式相加可证.
,然后所有不等式相加可证.
详解: (1)∵y=f(x)-g(x)=ln(ax+1)-![]() ,
,
y′=![]() -
-![]() =
=![]() ,
,
当a≥1时,y′≥0,所以函数y=f(x)-g(x)是[0,+∞)上的增函数;
当0<a<1时,由y′>0得x>2![]() ,所以函数y=f(x)-g(x)在
,所以函数y=f(x)-g(x)在 上是单调递增函数,函数y=f(x)-g(x)在
上是单调递增函数,函数y=f(x)-g(x)在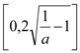 上是单调递减函数;
上是单调递减函数;
(2)当a≥1时,函数y=f(x)-g(x)是[0,+∞)上的增函数.
所以f(x)-g(x)≥f(0)-g(0)=1,
即不等式f(x)≥g(x)+1在x∈[0,+∞)时恒成立,
当0<a<1时,函数y=f(x)-g(x)是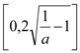 上的减函数,存在
上的减函数,存在 ,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
综上,实数a的取值范围是[1,+∞).
(3)当a=1时,由(2)得不等式f(x)>g(x)+1在x∈(0,+∞)时恒成立,
即ln(x+1)>![]() ,所以
,所以![]() ,
,
即![]() <
<![]() [ln(k+1)-lnk].
[ln(k+1)-lnk].
所以![]() <
<![]() (ln2-ln1),
(ln2-ln1),
![]() <
<![]() (ln3-ln2),
(ln3-ln2),
![]() <
<![]() (ln4-ln3),…,
(ln4-ln3),…,
![]() <
<![]() [ln(n+1)-lnn].
[ln(n+1)-lnn].
将上面各式相加得到,![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() [(ln2-ln1)+(ln3-ln2)+(ln4-ln3)+…+(ln(n+1)-lnn)]=
[(ln2-ln1)+(ln3-ln2)+(ln4-ln3)+…+(ln(n+1)-lnn)]=![]() ln(n+1)=
ln(n+1)=![]() f(n).
f(n).
∴原不等式成立.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)的导函数为f′(x),若f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2(e是自然对数的底数).
x2(e是自然对数的底数).
(1)求f(0)和f′(1)的值;
(2)若g(x)=![]() x2+a与函数f(x)的图象在区间[﹣1,2]上恰有2两个不同的交点,求实数a的取值范围.
x2+a与函数f(x)的图象在区间[﹣1,2]上恰有2两个不同的交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有初级教师21人,中级教师14人,高级教师7人,现采用分层抽样的方法从这些教师中抽取6人对绩效工资情况进行调查.
(1)求应从初级教师,中级教师,高级教师中分别抽取的人数;
(2)若从抽取的6名教师中随机抽取2名做进一步数据分析,求抽取的2名均为初级教师的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产能利用率是指实际产出与生产能力的比率,工r产能利用率是衡量工业生产经营状况的重要指标.下图为国家统计局发布的2015年至2018年第2季度我国工业产能利用率的折线图.
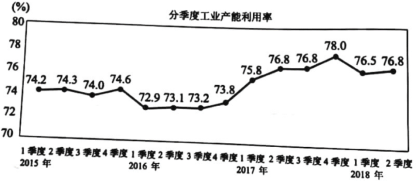
在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2016年第二季度与2015年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2015年第二季度与2015年第一季度相比较.
据上述信息,下列结论中正确的是( ).
A. 2015年第三季度环比有所提高B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高D. 2018年第一季度环比有所提高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() (不在y轴上).
(不在y轴上).

(1)若直线![]() 的斜率为3,求
的斜率为3,求![]() 的长度;
的长度;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值,并求出该定值;
为定值,并求出该定值;
(3)设![]() 的中点为
的中点为![]() ,是否存在直线
,是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为去广西桂林的某旅游团包飞机去旅游,其中旅行社的包机费为10000元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在20或20以下,飞机票每人收费800元;若旅游团的人数多于20,则实行优惠方案,每多1人,机票费每张减少10元,但旅游团的人数最多为75,则该旅行社可获得利润的最大值为( )
A. 12000元B. 15000元C. 12500元D. 20000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com