
ЁОЬтФПЁПаТНЎаЁФЯЙЯвдЩГЬ№ЮХУћШЋЙњЃЌаЁЬяМЦЛЎДгаТНЎдЫЪфаЁФЯЙЯШЅЩЯКЃЃЌЫцЛњДгФГЙЯХЉЕФЙЯЕиРяЬєбЁСЫ100ИіЃЌЦфжЪСПЗжБ№дк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЈЕЅЮЛЃКПЫЃЉжаЃЌОЭГМЦЕУЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌНЋЦЕТЪЪгЮЊИХТЪ.
ЃЈЕЅЮЛЃКПЫЃЉжаЃЌОЭГМЦЕУЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌНЋЦЕТЪЪгЮЊИХТЪ.
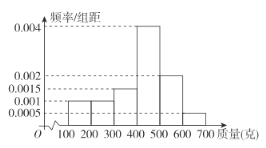
ЃЈ1ЃЉЧыИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦИУЙЯХЉЕФаЁФЯЙЯЕФЦНОљжЪСПЃЛ
ЃЈ2ЃЉвбжЊЙЯЕиРяЛЙга2ЭђИіаЁФЯЙЯвбОГЩЪьЃЌПЩвдВЩеЊЃЌаЁЬяЯыШЋВПЙКТђЃЌПЩЪЧЙЯХЉвЊЧѓГЌЙ§400ПЫЕФаЁФЯЙЯвд5дЊвЛИіЕФМлИёГіЪлЃЌЦфЫћЕФвд3дЊвЛИіЕФМлИёГіЪл.НЋЦЕТЪЪгЮЊИХТЪЃЌШєаТНЎЕНЩЯКЃЭљЗЕЕФдЫЗбдМ2000дЊЃЌЧыЮЪет2ЭђИіаЁФЯЙЯдкЩЯКЃвдУПНяЃЈ500ПЫЃЉЖрЩйдЊЖЈМлВХФмБЃжЄаЁЬяЕФРћШѓВЛЩйгк5000дЊЃПЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ3ЃЉФГЬьЭѕАЂвЬдкЩЯКЃФГГЌЪаЕФЪпВЫЙёЬЈЩЯПДЕНаЁЬяДгаТНЎВЩеЊЕФаТНЎаЁФЯЙЯЃЌвбжЊЙёЬЈЩЯгаШєИЩИіЃЌШєжЪСПГЌЙ§500ПЫЕФаЁФЯЙЯЮЊЁАгХжЪЦЗЁБЃЌЭѕАЂвЬЫцЛњЙКТђСЫ20ИіаЁФЯЙЯЃЌЧѓЭѕАЂвЬЙКТђЕФаЁФЯЙЯжаЁАгХжЪЦЗЁБИіЪ§ЕФЦкЭћ.
ЁОД№АИЁПЃЈ1ЃЉ415ПЫЃЛЃЈ2ЃЉжСЩйЖЈМлУПНя5.6дЊЃЛЃЈ3ЃЉ5
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнУПзщШЁжаЕуЮЊДњБэЃЌИљОнЦНОљЪ§ЕФЖЈвхНјааЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЧѓГіУПИіаЁФЯЙЯжЪСПГЌЙ§400ПЫЕФИХТЪЃЌдйЧѓГі2ЭђИіаЁФЯЙЯжажЪСПГЌЙ§400ПЫЕФИіЪ§ЃЌзюКѓНсКЯвбжЊЬѕМўНјааЧѓНтМДПЩЃЛ
ЃЈ3ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩЧѓГіаЁФЯЙЯжЪСПГЌЙ§500ПЫЕФИХТЪЃЌНсКЯЖўЯюЗжВМЕФаджЪНјааЧѓНтМДПЩ.
ЃЈ1ЃЉаЁФЯЙЯЕФЦНОљжЪСПЮЊ
![]() ЃЈПЫЃЉ
ЃЈПЫЃЉ
ЃЈ2ЃЉУПИіаЁФЯЙЯжЪСПГЌЙ§400ПЫЕФИХТЪЮЊ0.65ЃЌ
ЙЪ2ЭђИіаЁФЯЙЯжажЪСПГЌЙ§400ПЫЕФИіЪ§ЮЊ13000ИіЃЌ
МлжЕЮЊ![]() ЃЈдЊЃЉЃЌжЪСПЕЭгк400ПЫЕФМлжЕЮЊ
ЃЈдЊЃЉЃЌжЪСПЕЭгк400ПЫЕФМлжЕЮЊ![]() ЃЈдЊЃЉЃЌ
ЃЈдЊЃЉЃЌ
дђаЁЬядЫЕНЩЯКЃзмЕФЗбгУЮЊ![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
гЩЃЈ1ЃЉжЊЃЌ2ЭђИіаЁФЯЙЯЕФзмжЪСПЮЊ![]() ЃЈНяЃЉЃЌ
ЃЈНяЃЉЃЌ
вђЮЊ![]() ЃЌЫљвдаЁЬяжСЩйЖЈМлУПНя5.6дЊВХФмБЃжЄРћШѓВЛЩйгк5000дЊ.
ЃЌЫљвдаЁЬяжСЩйЖЈМлУПНя5.6дЊВХФмБЃжЄРћШѓВЛЩйгк5000дЊ.
ЃЈ3ЃЉгЩЦЕТЪЗжВМжБЗНЭМжЊЃЌаЁФЯЙЯжЪСПГЌЙ§500ПЫЕФИХТЪ![]() ЃЌ
ЃЌ
гЩЬтвтжЊЃЌЭѕАЂвЬЙКТђЕФаЁФЯЙЯжаЁАгХжЪЦЗЁБИіЪ§XЗўДгЖўЯюЗжВМ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
ЙЪЭѕАЂвЬЙКТђЕФаЁФЯЙЯжаЁАгХжЪЦЗЁБИіЪ§ЕФЦкЭћЮЊ5.


 гХЕШЩњЬтПтЯЕСаД№АИ
гХЕШЩњЬтПтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() ЃК
ЃК ![]() КЭХзЮяЯп
КЭХзЮяЯп![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЮЊзјБъдЕуЃЎ
ЮЊзјБъдЕуЃЎ
ЃЈ1ЃЉвбжЊжБЯп![]() КЭдВ
КЭдВ![]() ЯрЧаЃЌгыХзЮяЯп
ЯрЧаЃЌгыХзЮяЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧвТњзу
СНЕуЃЌЧвТњзу![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§ХзЮяЯп![]() ЩЯвЛЕу
ЩЯвЛЕу![]() зїСНжБЯп
зїСНжБЯп![]() КЭдВ
КЭдВ![]() ЯрЧаЃЌЧвЗжБ№НЛХзЮяЯп
ЯрЧаЃЌЧвЗжБ№НЛХзЮяЯп![]() гк
гк![]() СНЕуЃЌШєжБЯп
СНЕуЃЌШєжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЭждВCЃК![]() ЕФгвзМЯпЗНГЬЮЊxЃН2ЃЌЧвСННЙЕугыЖЬжсЕФвЛИіЖЅЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЎ
ЕФгвзМЯпЗНГЬЮЊxЃН2ЃЌЧвСННЙЕугыЖЬжсЕФвЛИіЖЅЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈ2ЃЉМйЩшжБЯпlЃК![]() гыЭждВCНЛгкAЃЌBСНЕуЃЎЂйШєAЮЊЭждВЕФЩЯЖЅЕуЃЌMЮЊЯпЖЮABжаЕуЃЌСЌНгOMВЂбгГЄНЛЭждВCгкNЃЌВЂЧв
гыЭждВCНЛгкAЃЌBСНЕуЃЎЂйШєAЮЊЭждВЕФЩЯЖЅЕуЃЌMЮЊЯпЖЮABжаЕуЃЌСЌНгOMВЂбгГЄНЛЭждВCгкNЃЌВЂЧв![]() ЃЌЧѓOBЕФГЄЃЛЂкШєдЕуOЕНжБЯпlЕФОрРыЮЊ1ЃЌВЂЧв
ЃЌЧѓOBЕФГЄЃЛЂкШєдЕуOЕНжБЯпlЕФОрРыЮЊ1ЃЌВЂЧв![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓЁїOABЕФУцЛ§SЕФЗЖЮЇЃЎ
ЪБЃЌЧѓЁїOABЕФУцЛ§SЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉШєжБЯп![]() дкЕу
дкЕу![]() ДІЧаЯпЗНГЬЮЊ
ДІЧаЯпЗНГЬЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉШєКЏЪ§![]() га3ИіСуЕуЃЌЧѓЪЕЪ§
га3ИіСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃН|2xЉa|+|xЉa+1|ЃЎ
ЃЈ1ЃЉЕБaЃН4ЪБЃЌЧѓНтВЛЕШЪНfЃЈxЃЉЁн8ЃЛ
ЃЈ2ЃЉвбжЊЙигкxЕФВЛЕШЪНfЃЈxЃЉ![]() дкRЩЯКуГЩСЂЃЌЧѓВЮЪ§aЕФШЁжЕЗЖЮЇЃЎ
дкRЩЯКуГЩСЂЃЌЧѓВЮЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвджБНЧзјБъЯЕЕФдЕуЮЊМЋЕуЃЌ![]() жсЕФЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌВЂдкСНжжзјБъЯЕжаШЁЯрЭЌЕФГЄЖШЕЅЮЛ.вбжЊЧњЯп
жсЕФЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌВЂдкСНжжзјБъЯЕжаШЁЯрЭЌЕФГЄЖШЕЅЮЛ.вбжЊЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЌ
ЮЊВЮЪ§ЃЌ![]() ЃЉЃЌЩфЯп
ЃЉЃЌЩфЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№гыЧњЯп
ЗжБ№гыЧњЯп![]() НЛгкМЋЕу
НЛгкМЋЕу![]() ЭтЕФШ§Еу
ЭтЕФШ§Еу![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() СНЕудкЧњЯп
СНЕудкЧњЯп![]() ЩЯЃЌЧѓ
ЩЯЃЌЧѓ![]() гы
гы![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФДЈЪЁЫЋСїжабЇЪЧвЛЫљЙњМвМЖЪОЗЖИпжаЃЌОпгагЦОУЕФАьбЇРњЪЗЁЂЗсИЛЕФАьбЇОбщ.НќФъРДЃЌЫЋжаЙВЮЊЙњФкЭтИпаЃЪфЫЭКЯИёаТЩњ20000грУћЃЌЦфжаЮЊЧхЛЊЁЂББДѓЁЂИДЕЉЁЂШЫДѓЕШвЛСїбЇИЎЪфЫЭаТЩњ1800грУћЃЌЩЯБОПЦЯпШЫЪ§ФъФъГЌЙ§ЧЇШЫЃЌХрбјГіЪЁЁЂЪаЁЂЯиИпПМЙкОќ17УћЃЌЮЛОгГЩЖМЪаЭЌРрбЇаЃЧАУЉ.ИУаЃИпШ§ФГАрга50УћбЇЩњВЮМгСЫНёФъГЩЖМЪаЁАвЛеяЁБПМЪдЃЌЦфжагЂгяГЩМЈЗўДге§ЬЌЗжВМ![]() ЃЌЪ§бЇГЩМЈЕФЦЕТЪЗжВМжБЗНЭМШчЯТЃК
ЃЌЪ§бЇГЩМЈЕФЦЕТЪЗжВМжБЗНЭМШчЯТЃК
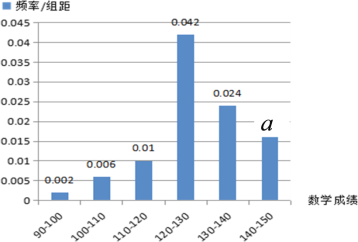
ЃЈ1ЃЉШчЙћГЩМЈ140ЗжМАвдЩЯЮЊЕЅПЦЬигХЃЌдђИУАрБОДЮПМЪджагЂгяЁЂЪ§бЇЕЅПЦЬигХДѓдМИїЖрЩйШЫЃП
ЃЈ2ЃЉЪдЮЪИУАрБОДЮПМЪджагЂгяКЭЪ§бЇЦНОљГЩМЈФФИіНЯИпЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЙћгЂгяКЭЪ§бЇСНПЦЖМЮЊЕЅПЦЬигХЙВга5ШЫЃЌАбЃЈ1ЃЉжаЕФНќЫЦЪ§зїЮЊецЪЕжЕЃЌДгЃЈ1ЃЉжаетаЉЭЌбЇжаЫцЛњГщШЁ3ШЫЃЌЩшШ§ШЫжагЂгяКЭЪ§бЇЫЋПЦЬигХЕФга![]() ШЫЃЌЧѓ
ШЫЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ВЮПМЙЋЪНМАЪ§ОнЃК
![]() дђ
дђ
![]()
![]()
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() гыКЏЪ§
гыКЏЪ§![]() КЭ
КЭ![]() ЖМЯрЧаЃЌдђВЛЕШЪНзщ
ЖМЯрЧаЃЌдђВЛЕШЪНзщ![]() ЫљШЗЖЈЕФЦНУцЧјгђдк
ЫљШЗЖЈЕФЦНУцЧјгђдк![]() ФкЕФУцЛ§ЮЊЃЈ ЃЉ
ФкЕФУцЛ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕк7НьЪРНчОќШЫдЫЖЏЛсгк2019Фъ10дТ18ШежС27ШедкКўББЮфККОйааЃЌШќЦк10ЬьЃЌЙВЩшжУЩфЛїЁЂгЮгОЁЂЬяОЖЁЂРКЧђЕШ27ИіДѓЯюЃЌ329ИіаЁЯю.ЙВгаРДзд100ЖрИіЙњМвЕФНќЭђУћЯжвлОќШЫЭЌЬЈОКММ.ЧАЦкЮЊгНгОќдЫЛсЫГРћейПЊЃЌЮфККЪаКмЖрЕЅЮЛКЭВПУХЖМПЊеЙСЫЗсИЛЖрВЪЕФаћДЋКЭНЬг§ЛюЖЏЃЌХЌСІШУДѓМвИќЖрЕФСЫНтОќдЫЛсЕФЯрЙижЊЪЖЃЌВЂГЋвщДѓМвзіЮФУїЙЋУё.ЮфККЪаЬхг§ОжЮЊСЫНтЙуДѓУёжкЖдОќдЫЛсжЊЪЖЕФжЊЯўЧщПіЃЌдкШЋЪаПЊеЙСЫЭјЩЯЮЪОэЕїВщЃЌУёжкВЮгыЖШМЋИпЃЌЯжДгДѓХњВЮгыепжаЫцЛњГщШЁ200УћавдЫВЮгыепЃЌЫћУЧЕУЗжЃЈТњЗж100ЗжЃЉЪ§ОнЃЌЭГМЦНсЙћШчЯТЃК
зщБ№ |
|
|
|
|
|
|
|
ЦЕЪ§ | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
ЃЈ1ЃЉШєДЫДЮЮЪОэЕїВщЕУЗжећЬхЗўДге§ЬЌЗжВМЃЌгУбљБОРДЙРМЦзмЬхЃЌЩш![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊет200ШЫЕУЗжЕФЦНОљжЕКЭБъзМВюЃЈЭЌвЛзщЪ§ОнгУИУЧјМфжаЕужЕзїЮЊДњБэЃЉЃЌЧѓ
ЗжБ№ЮЊет200ШЫЕУЗжЕФЦНОљжЕКЭБъзМВюЃЈЭЌвЛзщЪ§ОнгУИУЧјМфжаЕужЕзїЮЊДњБэЃЉЃЌЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЈ
ЕФжЕЃЈ![]() ЃЌ
ЃЌ![]() ЕФжЕЫФЩсЮхШыШЁећЪ§ЃЉЃЌВЂМЦЫу
ЕФжЕЫФЩсЮхШыШЁећЪ§ЃЉЃЌВЂМЦЫу![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЮЊИааЛДѓМвВЮгыетДЮЛюЖЏЃЌЪаЬхг§ОжЛЙЖдВЮМгЮЪОэЕїВщЕФавдЫЪаУёжЦЖЈШчЯТНБРјЗНАИЃКЕУЗжЕЭгк![]() ЕФПЩвдЛёЕУ1ДЮГщНБЛњЛсЃЌЕУЗжВЛЕЭгк
ЕФПЩвдЛёЕУ1ДЮГщНБЛњЛсЃЌЕУЗжВЛЕЭгк![]() ЕФПЩЛёЕУ2ДЮГщНБЛњЛсЃЌдквЛДЮГщНБжаЃЌГщжаМлжЕЮЊ15дЊЕФМЭФюЦЗAЕФИХТЪЮЊ
ЕФПЩЛёЕУ2ДЮГщНБЛњЛсЃЌдквЛДЮГщНБжаЃЌГщжаМлжЕЮЊ15дЊЕФМЭФюЦЗAЕФИХТЪЮЊ![]() ЃЌГщжаМлжЕЮЊ30дЊЕФМЭФюЦЗBЕФИХТЪЮЊ
ЃЌГщжаМлжЕЮЊ30дЊЕФМЭФюЦЗBЕФИХТЪЮЊ![]() .ЯжгаЪаУёеХЯШЩњВЮМгСЫДЫДЮЮЪОэЕїВщВЂГЩЮЊавдЫВЮгыепЃЌМЧYЮЊЫћВЮМгЛюЖЏЛёЕУМЭФюЦЗЕФзмМлжЕЃЌЧѓYЕФЗжВМСаКЭЪ§бЇЦкЭћЃЌВЂЙРЫуДЫДЮМЭФюЦЗЫљашвЊЕФзмН№Жю.
.ЯжгаЪаУёеХЯШЩњВЮМгСЫДЫДЮЮЪОэЕїВщВЂГЩЮЊавдЫВЮгыепЃЌМЧYЮЊЫћВЮМгЛюЖЏЛёЕУМЭФюЦЗЕФзмМлжЕЃЌЧѓYЕФЗжВМСаКЭЪ§бЇЦкЭћЃЌВЂЙРЫуДЫДЮМЭФюЦЗЫљашвЊЕФзмН№Жю.
ЃЈВЮПМЪ§ОнЃК![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() .ЃЉ
.ЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com