
【题目】(2015·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.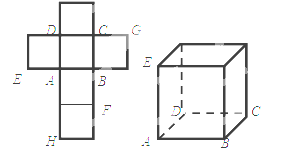
(1)请按字母F , G , H标记在正方体相应地顶点处(不需要说明理由)
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(3)证明:直线DF⊥平面BEG
【答案】
(1)
点F、G、H的位置如图所示.
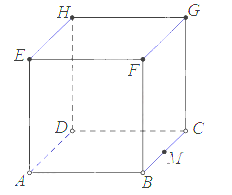
(2)
平面BEG∥平面ACH
(3)
见解析
【解析】(I)
点F、G、H的位置如图所示.
(II)平面BEG∥平面ACH.证明如下
因为ABCD-EFGH为正方体,所以BC∥FG , BC=FG
又FG∥EH , FG=EH , 所以BC∥EH , BC=EH
于是BCEH为平行四边形
所以BE∥CH
又CH![]() 平面ACH , BE平面ACH ,
平面ACH , BE平面ACH ,
所以BE∥平面ACH
同理BG∥平面ACH
又BE∩BG=B
所以平面BEG∥平面ACH
(Ⅲ)连接FH
因为ABCD-EFGH为正方体,所以DH⊥平面EFGH
因为EG![]() 平面EFGH , 所以DH⊥EG
平面EFGH , 所以DH⊥EG
又EG⊥FH , EG∩FH=O , 所以EG⊥平面BFHD
又DF![]() 平面BFDH , 所以DF⊥EG
平面BFDH , 所以DF⊥EG
同理DF⊥BG
又EG∩BG=G
所以DF⊥平面BEG.
【考点精析】掌握简单空间图形的三视图是解答本题的根本,需要知道画三视图的原则:长对齐、高对齐、宽相等.


科目:高中数学 来源: 题型:
【题目】已知关于的不等式![]() 的解集为
的解集为![]() ;
;
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若存在两个不相等负实数![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,满足:“对于任意
,满足:“对于任意![]() ,都有
,都有![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ”,若存在,求出
”,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 新课标II)已知椭圆C:9x2+y2=m2(m
新课标II)已知椭圆C:9x2+y2=m2(m![]() 0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
(1)(I)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)(II)若l过点(![]() ,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.

求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,椭圆E:![]() 的离心率是
的离心率是![]() ,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行与x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行与x轴时,直线l被椭圆E截得的线段长为2![]() .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 福建)“对任意x
福建)“对任意x![]()
![]() ,ksinxcosx<x”是“k<1”的( )
,ksinxcosx<x”是“k<1”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com