
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.分析 (Ⅰ)将M和N点坐标代入椭圆方程,根据斜率公式求得kMN=1,求得a和b的关系,当直线AP平行于x轴时,设|AC|=2d,求得A点坐标,代入椭圆方程,即可求得a和b,求得椭圆方程;
(Ⅱ)设出A、B、C和D点坐标,由向量共线,$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,及A和B在椭圆上,利用斜率公式,kAB=kCD,求得3(1+λ)kAB=-2(1+λ),即可求得kAB为定值.
解答 解:(Ⅰ)设M(m1,n1)、N(m2,n2),则$\left\{\begin{array}{l}{b^2}m_1^2+{a^2}n_1^2={a^2}{b^2}\\{b^2}m_2^2+{a^2}n_2^2={a^2}{b^2}\end{array}\right.$,
两式相减${k_{MN}}=\frac{{{n_1}-{n_2}}}{{{m_1}-{m_2}}}=-\frac{{{b^2}({m_1}+{m_2})}}{{{a^2}({n_1}+{n_2})}}=-\frac{{{b^2}×(-1)}}{{{a^2}×\frac{1}{3}}}=\frac{{3{b^2}}}{a^2}=1$,
故a2=3b2…(2分)
当直线AP平行于x轴时,设|AC|=2d,
∵$P(1,\frac{1}{2})$,$λ=\frac{1}{5}$,则$\frac{{|{AP}|}}{{|{PC}|}}=\frac{d-1}{d+1}=\frac{1}{5}$,解得$d=\frac{3}{2}$,
故点A(或C)的坐标为$(\frac{3}{2},\frac{1}{2})$.
代入椭圆方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,得$\frac{9}{{4{a^2}}}+\frac{1}{{4{b^2}}}=1$…4分
a2=3,b2=1,
所以方程为$\frac{x^2}{3}+{y^2}=1$…(6分)
(Ⅱ)设A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)
由于$\overrightarrow{AP}=λ\overrightarrow{PC}$,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
$\left\{\begin{array}{l}{x_P}=1=\frac{{{x_1}+λ{x_3}}}{1+λ}\\{y_P}=\frac{1}{2}=\frac{{{y_1}+λ{y_3}}}{1+λ}\end{array}\right.⇒\left\{\begin{array}{l}{x_1}+λ{x_3}=1+λ\\{y_1}+λ{y_3}=\frac{1}{2}(1+λ)\end{array}\right.$…①
同理$\overrightarrow{BP}=λ\overrightarrow{PD}$可得$\left\{\begin{array}{l}{x_2}+λ{x_4}=1+λ\\{y_2}+λ{y_4}=\frac{1}{2}(1+λ)\end{array}\right.$…②…(8分)
由①②得:$\left\{\begin{array}{l}{x_1}+{x_2}+λ({x_3}+{x_4})=2(1+λ)\\{y_1}+{y_2}+λ({y_3}+{y_4})=(1+λ)\end{array}\right.$…③
将点A、B的坐标代入椭圆方程得$\left\{\begin{array}{l}x_1^2+3y_1^2=3\\ x_2^2+3y_2^2=3\end{array}\right.$,
两式相减得(x1+x2)(x1-x2)+3(y1+y2)(y1-y2)=0,
于是3(y1+y2)kAB=-(x1+x2)…④
同理可得:3(y3+y4)kCD=-(x3+x4),…(10分)
于是3(y3+y4)kAB=-(x3+x4)(∵AB∥CD,∴kAB=kCD)
所以3λ(y3+y4)kAB=-λ(x3+x4)…⑤
由④⑤两式相加得到:3[y1+y2+λ(y3+y4)]kAB=-[(x1+x2)+λ(x3+x4)]
把③代入上式得3(1+λ)kAB=-2(1+λ),
解得:${k_{AB}}=-\frac{2}{3}$,
当λ变化时,kAB为定值,${k_{AB}}=-\frac{2}{3}$.…(12分)
点评 本题考查椭圆的标准方程的求法,考查直线的斜率斜率公式,向量共线定理,解题时要认真审题,注意点差法的合理运用,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
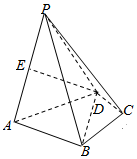 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )
一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
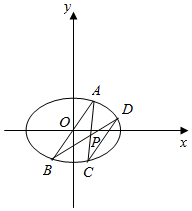 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
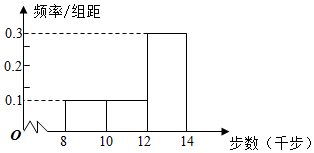 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com