
【题目】根据《山东省全民健身实施计划(2016-2020年)》,到2020年乡镇(街道)普遍建有“两个一”工程,即一个全民健身活动中心或灯光篮球场、一个多功能运动场.某市把甲、乙、丙、丁四个多功能运动场全部免费为市民开放.

(1)在一次全民健身活动中,四个多功能运动场的使用场数如图,用分层抽样的方法从甲、乙、丙、丁四场馆的使用场数中依次抽取![]() ,
,![]() ,
,![]() ,
,![]() 共25场,在
共25场,在![]() ,
,![]() ,
,![]() ,
,![]() 中随机取两数,求这两数和
中随机取两数,求这两数和![]() 的分布列和数学期望;
的分布列和数学期望;
(2)设四个多功能运动场一个月内各场使用次数之和为![]() ,其相应维修费用为
,其相应维修费用为![]() 元,根据统计,得到如下表的
元,根据统计,得到如下表的![]() 与
与![]() 数据:
数据:
| 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 2302 | 2708 | 2996 | 3219 | 3401 | 3555 | 3689 |
| 2.49 | 2.99 | 3.55 | 4.00 | 4.49 | 4.99 | 5.49 |
(i)用最小二乘法求![]() 与
与![]() 之间的回归直线方程;
之间的回归直线方程;
(ii)![]() 叫做运动场月惠值,根据(i)的结论,试估计这四个多功能运动场月惠值最大时
叫做运动场月惠值,根据(i)的结论,试估计这四个多功能运动场月惠值最大时![]() 的值.
的值.
参考数据和公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
 ,
,![]() .
.
【答案】(1)分布列见解析,![]() ;(2)(i)
;(2)(i)![]() ;(ii)20.
;(ii)20.
【解析】
(1)根据题意,确定抽样比,得到![]() ,
,![]() ,
,![]() ,
,![]() 的值分别为5,6,9,5;所以这两数和
的值分别为5,6,9,5;所以这两数和![]() 的所有可能的取值为10,11,14,15,求出对应概率,即可得出分布列与数学期望;
的所有可能的取值为10,11,14,15,求出对应概率,即可得出分布列与数学期望;
(2)(i)由最小二乘法,结合题中数据,求出![]() ,
,![]() 的估计值,从而可得回归直线方程;
的估计值,从而可得回归直线方程;
(ii)由(i)得到![]() ,所以
,所以![]() ,设
,设![]() ,用导数的方法求其最值即可.
,用导数的方法求其最值即可.
(1)根据题中所给的条形图,易知总场数为100,所以抽样比例为![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() 的值分别为5,6,9,5.
的值分别为5,6,9,5.
所以这两数和![]() 的所有可能的取值为10,11,14,15.
的所有可能的取值为10,11,14,15.
于是![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 10 | 11 | 14 | 15 |
|
|
|
|
|
所以![]() .
.
(2)(i)因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以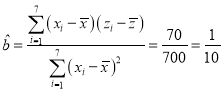 ,
,
即![]() ,
,
所以![]() 与
与![]() 之间的回归直线方程为
之间的回归直线方程为![]() .
.
(ii)因为![]() ,
,
所以![]() ,
,
设![]() ,
,
则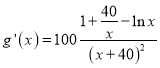 ,
,
令![]() ,
,![]() 在
在![]() 恒成立,
恒成立,
则![]() 在
在![]() 为减函数,又
为减函数,又![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以估计这四个多功能运动场月惠值最大时![]() 的值为20.
的值为20.


科目:高中数学 来源: 题型:
【题目】函数![]() 的最小正周期为
的最小正周期为![]() ,若其图象向左平移
,若其图象向左平移![]() 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数![]() 的图象( )
的图象( )
A.关于点![]() 对称B.关于点
对称B.关于点![]() 对称
对称
C.关于直线![]() 对称D.关于直线
对称D.关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府为了调查市民对A、B两服务部门的服务满意度情况,随机访问了50位市民,根据这50位市民对两部门的评分![]() 评分越高表明市民的满意度越高
评分越高表明市民的满意度越高![]() 绘制的茎叶图如图:
绘制的茎叶图如图:

则下列说法正确的是![]()
![]()
A.这50位市民对A、B两部门评分的方差,A部门的评分方差大
B.估计市民对A、B两部门的评分高于90的概率相同
C.这50位市民对A部门的评分其众数大于中位数
D.该市的市民对B部门评分中位数的估计值是67
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE及平面DEC都与平面ADE垂直.

(1)求证:BC∥平面ADE;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造.根据史书的记载和考古材料的发现,古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为![]() ,径粗
,径粗![]() ,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“
,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
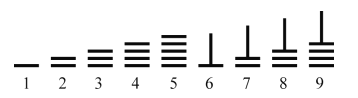
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将4本不同的书随机放入如图所示的编号为1,2,3,4的四个抽屉中.
1 | 2 | 3 | 4 |
(Ⅰ)求4本书恰好放在四个不同抽屉中的概率;
(Ⅱ)随机变量![]() 表示放在2号抽屉中书的本数,求
表示放在2号抽屉中书的本数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点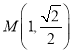 ,
,![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,与圆
两点,与圆![]() 相切与点
相切与点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)以线段![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() (
(![]() 是坐标原点),求实数
是坐标原点),求实数![]() 的取值范围;
的取值范围;
(3)![]() 是否为定值,如果是,求
是否为定值,如果是,求![]() 的值;如果不是,求
的值;如果不是,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com