
设A(xA,yA),B(xB,yB)为平面直角坐标系上的两点,其中xA,yA,xB,yBÎZ.令△x=xB-xA,△y=yB-yA,若|△x|+|△y|=3,且|△x|·|△y|≠0,则称点B为点A的“相关点”,记作:B=f(A).
(1)请问:点(0,0)的“相关点”有几个?判断这些点是否在同一个圆上,若在,写出圆的方程;若不在,说明理由;
(2)已知点H(9,3),L(5,3),若点M满足M=f(H),L=f(M),求点M的坐标;
(3)已知P0(x0,y0)(x0ÎZ,y0ÎZ)为一个定点, 若点Pi满足Pi=f (Pi-1),其中i=1,2,3,···,n,求|P0Pn|的最小值.
(1)x²+y²=5
(2)M(7,2)或M(7,4).
(3)当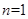 时, |P0Pn|的最小值为
时, |P0Pn|的最小值为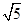 ;
;
当n=2k,kÎN *时, |P0Pn|的最小值为0;
当n=2k+1,kÎN *时, |P0Pn|的最小值为1.
【解析】
试题分析:解: (1)因为|△x|+|△y|=3(|△x|,|△y|为非零整数),
故|△x|=1,|△y|=2或|△x|=2,|△y|=1,所以点(0,0)的“相关点”有8个 .
又因为(△x)²+(△y)²=5,即(△x-0)²+(△y-0)²="5" .
所以这些可能值对应的点在以(0,0)为圆心,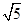 为半径的圆上,
为半径的圆上,
方程为x²+y²="5" . 3分
(2)设M(xM,yM),
因为M=f(H),L=f(M),
所以有|xM-9|+|yM-3|="3," |xM-5|+|yM-3|=3,
所以|xM-9|=|xM-5|,所以xM=7, yM=2或yM=4,
所以M(7,2)或M(7,4). 6分
(3) 当n=1时,可知|P0Pn|的最小值为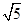 ;
;
当n=2k,kÎN *时, |P0Pn|的最小值为0 ;
当n=3时,对于点P,按照下面的方法选择“相关点”,可得P3(x0,y0+1):
P0(x0,y0)→P1(x0+2,y0+1)→P2(x0+1,y0+3) →P3(x0,y0+1)
故|P0Pn|的最小值为1,
当n=2k+3, kÎN *时,对于点P,经过2k次变换回到初始点P0(x0,y0),然后经过3次变换回到Pn(x0,y0+1),故|P0Pn|的最小值为1.
综上,当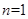 时, |P0Pn|的最小值为
时, |P0Pn|的最小值为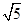 ;
;
当n=2k,kÎN *时, |P0Pn|的最小值为0;
当n=2k+1,kÎN *时, |P0Pn|的最小值为1. 10分
考点:圆的方程,两点距离
点评:主要是考查了圆的方程的求解,以及两点距离的最值,属于中档题。


科目:高中数学 来源: 题型:
| n |  | i=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:海淀区一模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年北京市海淀区高考数学一模试卷(理科)(解析版) 题型:解答题
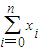 ,求T的最大值.
,求T的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com