
【题目】在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,则λ的取值范围是( )
,则λ的取值范围是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】下列命题: ①“若a2<b2 , 则a<b”的否命题;
②“全等三角形面积相等”的逆命题;
③“若a>1,则ax2﹣2ax+a+3>0的解集为R”的逆否命题;
④“若 ![]() x(x≠0)为有理数,则x为无理数”的逆否命题.
x(x≠0)为有理数,则x为无理数”的逆否命题.
其中正确的命题是( )
A.③④
B.①③
C.①②
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =({cosx,﹣
=({cosx,﹣ ![]() cosx),
cosx), ![]() =(cosx,sinx),函数f(x)=
=(cosx,sinx),函数f(x)= ![]()
![]() +1. (Ⅰ)求函数f(x)的单调递增区间;
+1. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若f(θ)= ![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用x代替,则这位运动员这8场比赛的得分平均数不小于得分中位数的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣2,an+1=2an+4.
(1)证明数列{an+4}是等比数列并求出{an}通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列一段材料,然后解答问题:对于任意实数x,符号[x]表示“不超过x的最大整数”,在数轴上,当x是整数,[x]就是x,当x不是整数时,[x]是点x左侧的第一个整数点,这个函数叫做“取整函数”,也叫高斯(Gauss)函数.如[﹣2]=﹣2,[﹣1.5]=﹣2,[2.5]=2.求[log2![]() ]+[log2
]+[log2![]() ]+[log2
]+[log2![]() ]+[log21]+[log22]+[log23]+[log24]的值为( )
]+[log21]+[log22]+[log23]+[log24]的值为( )
A.-1
B.-2
C.0
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直棱柱ABC﹣A1B1C1中,AC=BC=CC1= ![]() AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
(Ⅱ)求二面角E﹣AB1﹣C的大小.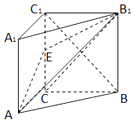
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com