
已知函数f(x)=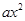 -(a+2)x+lnx.
-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e)上的最小值为-2,求a的取值范围.
(1)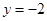 ;(2)
;(2)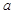 的取值范围为
的取值范围为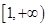 .
.
【解析】
试题分析:(1)求出函数解析式,根据导数几何意义解答即可;(2)求出函数导数令其等于零得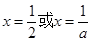 ,当
,当 ,即
,即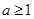 时,
时,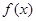 在[1,e]上单调递增,求出最小值验证,符合题意,当
在[1,e]上单调递增,求出最小值验证,符合题意,当 ,和
,和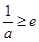 时其最小值都不是
时其最小值都不是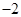 ,故不合题意,所以
,故不合题意,所以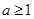 .
.
试题解析:(1)当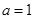 时,
时,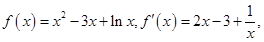 1分
1分
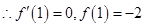 3分
3分
所以切线方程是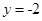 4分
4分
(2)函数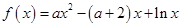 的定义域是
的定义域是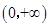
当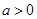 时,
时,
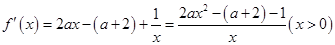 5分
5分
令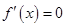 ,即
,即
所以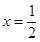 或
或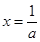 6分
6分
当 ,即
,即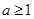 时,
时,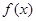 在[1,e]上单调递增,
在[1,e]上单调递增,
所以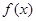 在[1,e]上的最小值是
在[1,e]上的最小值是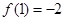 ;………………8分
;………………8分
当 时,
时,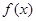 在[1,e]上的最小值是
在[1,e]上的最小值是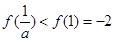 ,不合题意; 10分
,不合题意; 10分
当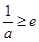 时,
时,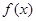 在[1,e]上单调递减,
在[1,e]上单调递减,
所以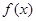 在[1,e]上的最小值是
在[1,e]上的最小值是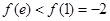 ,不合题意 11分
,不合题意 11分
故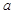 的取值范围为
的取值范围为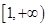 ; 12分
; 12分
考点:导数的几何意义、利用导数求函数最值.


科目:高中数学 来源: 题型:
(08年上虞市质检一文) 已知函数f(x)=ax4+bx2+c的图象经过点(0,2),且在x=1处的切线方程
是y=-4x+![]() .
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)在区间[-4,1]上的最值.查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三上学期期联考文科数学试卷(解析版) 题型:解答题
已知函数f(x)=2sin(ωx+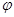 )(ω>0,0<
)(ω>0,0<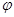 <π)的图象如图所示.
<π)的图象如图所示.

(1)求函数f(x)的解析式:
(2)已知 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值.
查看答案和解析>>
科目:高中数学 来源:2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=ln -a
-a +x(a>0).
+x(a>0).
(Ⅰ)若 =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;
(Ⅱ)若 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高三一轮精品复习单元测试(12)数学试卷解析版 题型:解答题
(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在x=-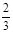 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com