
分析 由题意可得$\frac{1}{y}$=-$\frac{sinx-0}{cosx-2}$,$\frac{sinx-0}{cosx-2}$表示点A(2,0)和B(cosx,sinx)连线的斜率,数形结合可得$\frac{sinx-0}{cosx-2}$的最小值,由不等式的性质可得.
解答 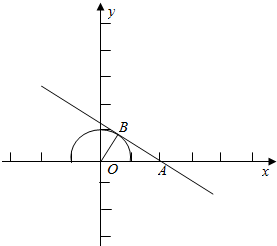 解:∵0<x<π,∴cosx∈(-1,1),
解:∵0<x<π,∴cosx∈(-1,1),
∴由y=$\frac{2-cosx}{sinx}$可得$\frac{1}{y}$=-$\frac{sinx-0}{cosx-2}$,
而$\frac{sinx-0}{cosx-2}$表示点A(2,0)和B(cosx,sinx)连线的斜率,
由0<x<π可得点B(cosx,sinx)在单位圆的上半个圆(不含端点),
数形结合可得当直线与上半圆相切时,$\frac{sinx-0}{cosx-2}$取最小值,
由OB=1,OA=2在RT△OAB中可得∠OAB=30°,
此时$\frac{sinx-0}{cosx-2}$=tan150°=-$\frac{\sqrt{3}}{3}$,即$\frac{sinx-0}{cosx-2}$≥-$\frac{\sqrt{3}}{3}$,
∴-$\frac{sinx-0}{cosx-2}$≤$\frac{\sqrt{3}}{3}$,∴$\frac{1}{y}$≤$\frac{\sqrt{3}}{3}$,∴y≥$\sqrt{3}$
故答案为:$\sqrt{3}$.
点评 本题考查三角函数的最值,转化为直线的斜率并数形结合是解决问题的关键,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
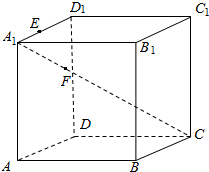 如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线.
如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com