
【题目】中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一![]() 名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分
名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分![]() 分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
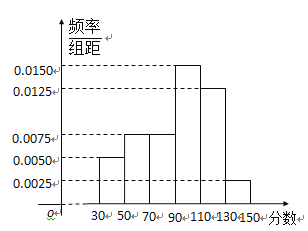
分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.

(1)填写答题卡频率分布表中的空格, 补全频率分布直方图, 并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点. 
(1)求证:EF⊥B1C;
(2)求三棱锥E﹣FCB1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化阶段,“老有所依”也是政府的民生工程.为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如图表.

(1)若采用分层抽样的方法,再从样本中不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)据统计该市大约有![]() 的户籍老人无固定收入,且在各健康状况人群中所占比例相同,政府计划每月为这部分老人发放生活补贴,标准如下:
的户籍老人无固定收入,且在各健康状况人群中所占比例相同,政府计划每月为这部分老人发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外再发放生活补贴100元.
若用频率估计概率,设任意户籍老人每月享受的生活补贴为![]() 元,求
元,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2 ![]() ,求直线l的方程
,求直线l的方程
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2 , 它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,求所有满足条件的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高三抽取了500名学生,记录了他们选修A、B、C三门课的选修情况,如表:
科目 学生人数 | A | B | C |
120 | 是 | 否 | 是 |
60 | 否 | 否 | 是 |
70 | 是 | 是 | 否 |
50 | 是 | 是 | 是 |
150 | 否 | 是 | 是 |
50 | 是 | 否 | 否 |
(Ⅰ)试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率.
(Ⅱ)若该高三某学生已选修A,则该学生同时选修B、C中哪门的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com