
分析 (1)求出函数的导数,解关于导函数的不等式求出函数的单调区间,从而求出函数的极值即可;
(2)求出h(x)的导数,通过讨论a的范围,求出函数的单调区间,从而进一步确定a的范围即可.
解答 解:(1)由题意可知f(x)的定义域为(0,+∞),…(1分)
当a=1时,f(x)=x-lnx,$f'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,…(3分)
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
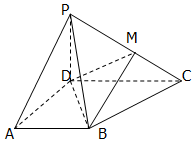 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )
已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )| A. | 67 | B. | 69 | C. | 73 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
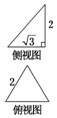 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )| A. | 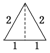 | B. |  | C. | 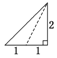 | D. | 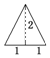 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com