
【题目】设△ABC的内角A,B,C 的对边分别是a,b,c,已知 b+acos C=0,sin A=2sin(A+C).
(1)求角C的大小;
(2)求 ![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】设向量 ![]() ,
, ![]() 的夹角为60°且|
的夹角为60°且| ![]() |=|
|=| ![]() |=1,如果
|=1,如果 ![]() ,
, ![]() ,
, ![]() .
.
(1)证明:A、B、D三点共线.
(2)试确定实数k的值,使k的取值满足向量 ![]() 与向量
与向量 ![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若(a+b+c)(b+c﹣a)=3ab,且sinA=2sinBcosC,那么△ABC是( )
A.直角三角形
B.等边三角形
C.等腰三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC 中,角A,B,C所对的边分別为a,b,c,且asin Acos C+csin AcosA= ![]() c
c
(1)若c=1,sin C= ![]() ,求△ABC的面积S
,求△ABC的面积S
(2)若D 是AC的中点且cosB= ![]() ,BD=
,BD= ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠BAD=90°,AD= ![]() ,DC=2AB=2,E为BC中点.
,DC=2AB=2,E为BC中点. 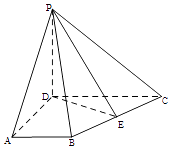
(1)求证:平面PBC⊥平面PDE
(2)线段PC上是否存在一点F,使PA∥平面BDF?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com