练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数，证明：

    （Ⅰ）对每个，存在唯一的，满足；

    （Ⅱ）对任意，由（Ⅰ）中构成的数列满足。

    【答案】 （Ⅰ） 见下.   （Ⅱ）见下.

    【解析】 （Ⅰ） 是x的单调递增函数,也是n的单调递增函数. .

    综上，对每个，存在唯一的，满足；(证毕)

    （Ⅱ） 由题知

    上式相减：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （04年广东卷）（12分）

    设函数

    (I)证明：当且时，

    (II)点（0<x0<1）在曲线上，求曲线上在点处的切线与轴，轴正向所围成的三角形面积的表达式。（用表示）

    查看答案和解析>>

    科目：高中数学 来源：2013年全国普通高等学校招生统一考试理科数学（安徽卷解析版） 题型：解答题

    设函数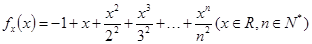，证明：

    （Ⅰ）对每个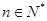，存在唯一的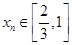，满足；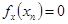

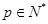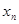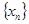    （Ⅱ）对任意，由（Ⅰ）中构成的数列满足.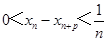

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省高三上学期期中考试数学试卷（解析版） 题型：解答题

    设函数.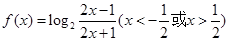

    (1)证明:是奇函数;

    (2)求的单调区间;

    (3)写出函数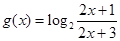图象的一个对称中心.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届北京西城（南区）高二下学期期末考试理科数学试卷（解析版） 题型：解答题

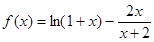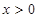    （Ⅰ）设函数，证明：当时，；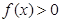

    （Ⅱ）从编号1到100的100张卡片中每次随机抽取一张，然后放回，用这种方式连续抽取20次，设抽得的20个号码互不相同的概率为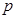。证明：。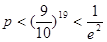

    注：可用（Ⅰ）的结论。

     

    查看答案和解析>>

    同步练习册答案