
ЁОЬтФПЁПЩш![]() ЪЧвЛИіЗЧПеМЏКЯЃЌ
ЪЧвЛИіЗЧПеМЏКЯЃЌ ![]() ЪЧЖЈвхдк
ЪЧЖЈвхдк![]() ЩЯЕФвЛИідЫЫу.ШчЙћЭЌЪБТњзуЯТЪіЫФИіЬѕМўЃК
ЩЯЕФвЛИідЫЫу.ШчЙћЭЌЪБТњзуЯТЪіЫФИіЬѕМўЃК
ЃЈ1ЃЉЖдгк![]() ЃЌЖМга
ЃЌЖМга![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЖдгк![]() ЃЌЖМга
ЃЌЖМга![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЖдгк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЖдгк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЈзЂЃКЁА
ЃЈзЂЃКЁА![]() ЁБЭЌЃЈiiiЃЉжаЕФЁА
ЁБЭЌЃЈiiiЃЉжаЕФЁА![]() ЁБЃЉ.
ЁБЃЉ.
дђГЦ![]() ЙигкдЫЫу
ЙигкдЫЫу![]() ЙЙГЩвЛИіШК.ЯжИјГіЯТСаМЏКЯКЭдЫЫуЃК
ЙЙГЩвЛИіШК.ЯжИјГіЯТСаМЏКЯКЭдЫЫуЃК
Ђй![]() ЪЧећЪ§МЏКЯЃЌ
ЪЧећЪ§МЏКЯЃЌ ![]() ЮЊМгЗЈЃЛЂк
ЮЊМгЗЈЃЛЂк![]() ЪЧЦцЪ§МЏКЯЃЌ
ЪЧЦцЪ§МЏКЯЃЌ ![]() ЮЊГЫЗЈЃЛЂл
ЮЊГЫЗЈЃЛЂл![]() ЪЧЦНУцЯђСПМЏКЯЃЌ
ЪЧЦНУцЯђСПМЏКЯЃЌ ![]() ЮЊЪ§СПЛ§дЫЫуЃЛЂм
ЮЊЪ§СПЛ§дЫЫуЃЛЂм![]() ЪЧЗЧСуИДЪ§МЏКЯЃЌ
ЪЧЗЧСуИДЪ§МЏКЯЃЌ ![]() ЮЊГЫЗЈ. Цфжа
ЮЊГЫЗЈ. Цфжа![]() ЙигкдЫЫу
ЙигкдЫЫу![]() ЙЙГЩШКЕФађКХЪЧ___________ЃЈНЋФуШЯЮЊе§ШЗЕФађКХЖМаДЩЯЃЉ.
ЙЙГЩШКЕФађКХЪЧ___________ЃЈНЋФуШЯЮЊе§ШЗЕФађКХЖМаДЩЯЃЉ.
ЁОД№АИЁПЂйЂм
ЁОНтЮіЁП![]() Шє
Шє![]() ЪЧећЪ§МЏКЯЃЌдђ
ЪЧећЪ§МЏКЯЃЌдђ![]() СНИіећЪ§ЯрМгШдЮЊећЪ§ЃЌ
СНИіећЪ§ЯрМгШдЮЊећЪ§ЃЌ ![]() ећЪ§МгЗЈТњзуНсКЯТЩЃЛ
ећЪ§МгЗЈТњзуНсКЯТЩЃЛ ![]()
![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ ![]() дкећЪ§МЏКЯжаДцдкЮЈвЛвЛИі
дкећЪ§МЏКЯжаДцдкЮЈвЛвЛИі![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙЪећЪ§МЏКЯЙигкдЫЫу*ЙЙГЩвЛИіШКЃЛ
ЃЌЙЪећЪ§МЏКЯЙигкдЫЫу*ЙЙГЩвЛИіШКЃЛ
![]() ЪЧЦцЪ§МЏКЯЃЌ
ЪЧЦцЪ§МЏКЯЃЌ ![]() ЮЊГЫЗЈЃЌдђ
ЮЊГЫЗЈЃЌдђ![]() ЃЌВЛТњзу
ЃЌВЛТњзу![]() ЃЛ
ЃЛ
![]() ЪЧЦНУцЯђСПМЏКЯЃЌ
ЪЧЦНУцЯђСПМЏКЯЃЌ ![]() ЮЊЪ§СПЛ§дЫЫуЃЌдђВЛТњзу
ЮЊЪ§СПЛ§дЫЫуЃЌдђВЛТњзу![]() ЃЛ
ЃЛ
![]() ЪЧЗЧСуИДЪ§МЏКЯЃЌ
ЪЧЗЧСуИДЪ§МЏКЯЃЌ ![]() ЮЊГЫЗЈЃЌдђ
ЮЊГЫЗЈЃЌдђ![]() СНИіЗЧСуИДЪ§ЯрГЫШдЮЊЗЧСуИДЪ§ЃЛ
СНИіЗЧСуИДЪ§ЯрГЫШдЮЊЗЧСуИДЪ§ЃЛ ![]() ЗЧСуИДЪ§ЯрГЫЗћКЯНсКЯТЩЃЛ
ЗЧСуИДЪ§ЯрГЫЗћКЯНсКЯТЩЃЛ ![]() ЃЌдђЃЉ
ЃЌдђЃЉ![]() ЃЛ
ЃЛ ![]() дк
дк![]() жаДцдкЮЈвЛвЛИі
жаДцдкЮЈвЛвЛИі![]() ЃЌЪЙ
ЃЌЪЙ![]() ЁЃ
ЁЃ
ЙЪД№АИЮЊ![]()
![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= ![]() ЃЈx2Љ2ax+3ЃЉЃЎ
ЃЈx2Љ2ax+3ЃЉЃЎ
ЃЈ1ЃЉШєfЃЈxЃЉЕФЖЈвхгђЮЊRЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєfЃЈЉ1ЃЉ=Љ3ЃЌЧѓfЃЈxЃЉЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§aЃЌЪЙfЃЈxЃЉдкЃЈЉЁоЃЌ2ЃЉЩЯЮЊдіКЏЪ§ЃПШєДцдкЃЌЧѓГіaЕФЗЖЮЇЃПШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ ![]() ЪЧ
ЪЧ![]() ЕФЕМКЏЪ§ЃЎ
ЕФЕМКЏЪ§ЃЎ
ЃЈЂёЃЉЧѓ![]() ЕФМЋжЕЃЛ
ЕФМЋжЕЃЛ
ЃЈЂђЃЉШє![]() дк
дк![]() ЪБКуГЩСЂЃЌЧѓЪЕЪ§
ЪБКуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКy2=2pxЃЈpЃО0ЃЉЃЌЩЯЕФЕуMЃЈ1ЃЌmЃЉЕНЦфНЙЕуFЕФОрРыЮЊ2ЃЌ
ЃЈ1ЃЉЧѓCЕФЗНГЬЃЛВЂЧѓЦфзМЯпЗНГЬЃЛ
ЃЈ2ЃЉвбжЊA ЃЈ1ЃЌЉ2ЃЉЃЌЪЧЗёДцдкЦНаагкOAЃЈOЮЊзјБъдЕуЃЉЕФжБЯпLЃЌЪЙЕУжБЯпLгыХзЮяЯпCгаЙЋЙВЕуЃЌЧвжБЯпOAгыLЕФОрРыЕШгк ![]() ЃПШєДцдкЃЌЧѓжБЯпLЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓжБЯпLЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМИјГіЕФЪЧМЦЫу ![]() ЕФжЕЕФвЛИіГЬађПђЭМЃЌХаЖЯЦфжаПђФкгІЬюШыЕФЬѕМўЪЧЃЈ ЃЉ
ЕФжЕЕФвЛИіГЬађПђЭМЃЌХаЖЯЦфжаПђФкгІЬюШыЕФЬѕМўЪЧЃЈ ЃЉ 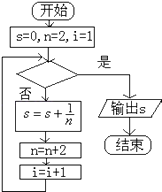
A.iЃО10
B.iЃМ10
C.iЃО20
D.iЃМ20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() КЭжБЯп
КЭжБЯп![]() ЃК
ЃК ![]() ЃЌЭждВЕФРыаФТЪ
ЃЌЭждВЕФРыаФТЪ![]() ЃЌзјБъдЕуЕНжБЯп
ЃЌзјБъдЕуЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() .
.
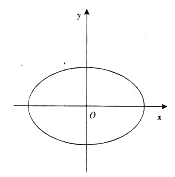
ЃЈЂёЃЉЧѓЭждВЕФЗНГЬЃЛ
ЃЈЂђЃЉвбжЊЖЈЕу![]() ЃЌШєжБЯп
ЃЌШєжБЯп![]() Й§Еу
Й§Еу![]() ЧвгыЭждВЯрНЛгк
ЧвгыЭждВЯрНЛгк![]() СНЕуЃЌЪдХаЖЯЪЧЗёДцдкжБЯп
СНЕуЃЌЪдХаЖЯЪЧЗёДцдкжБЯп![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЮЊжБОЖЕФдВЙ§Еу
ЮЊжБОЖЕФдВЙ§Еу![]() ЃПШєДцдкЃЌЧѓГіжБЯп
ЃПШєДцдкЃЌЧѓГіжБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=|2x+1|Љ|xЉ4|ЃЎ
ЃЈ1ЃЉНтВЛЕШЪНfЃЈxЃЉЃО0ЃЛ
ЃЈ2ЃЉШєfЃЈxЃЉ+3|xЉ4|ЃОmЖдвЛЧаЪЕЪ§xОљГЩСЂЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧе§ЫФУцЬхЕФЦНУцеЙПЊЭМЃЌGЃЌHЃЌMЃЌNЗжБ№ЮЊDEЃЌBEЃЌEFЃЌECЕФжаЕуЃЌдкетИіе§ЫФУцЬхжаЃЌ
ЂйGHгыEFЦНааЃЛЂкBDгыMNЮЊвьУцжБЯпЃЛЂлGHгыMNГЩ60ЁуНЧЃЛЂмDEгыMNДЙжБЃЎвдЩЯЫФИіУќЬтжаЃЌе§ШЗУќЬтЕФађКХЪЧ ЃЎ 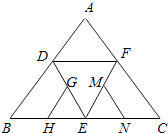
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ1ЃЉ Йигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() дкЧјМф
дкЧјМф![]() ЩЯгаНт,Чѓ
ЩЯгаНт,Чѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉ ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() КуГЩСЂ,ЧѓЪЕЪ§
КуГЩСЂ,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com