
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方![]() ,且直线l与曲线C相交于A,B两点.
,且直线l与曲线C相交于A,B两点.
(1)求曲线C的普通方程和l的直角坐标方程;
(2)若![]() ,点
,点![]() 满足
满足![]() ,求此时r的值.
,求此时r的值.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】在《周髀算经》中,把圆及其内接正方形称为圆方图,把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑,它的正面图如图所示.以该木塔底层的边![]() 作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点
作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点![]() 正好位于塔身和塔顶的分界.经测量发现,木塔底层的边
正好位于塔身和塔顶的分界.经测量发现,木塔底层的边![]() 不少于
不少于![]() 米,塔顶
米,塔顶![]() 到点
到点![]() 的距离不超过
的距离不超过![]() 米,则该木塔的高度可能是(参考数据:
米,则该木塔的高度可能是(参考数据:![]() )( )
)( )

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中![]() 表示这些半音的频率,它们满足
表示这些半音的频率,它们满足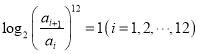 .若某一半音与
.若某一半音与![]() 的频率之比为
的频率之比为![]() ,则该半音为( )
,则该半音为( )
频率 |
|
|
|
|
|
|
|
|
|
|
|
| |
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项数学竞赛考试共四道题,考察内容分别为代数、几何、数论、组合,已知前两题每题满分40分,后两题每题满分60分,题目难度随题号依次递增,已知学生甲答题时,若该题会做则必得满分,若该题不会做则不作答得0分,通过对学生甲以往测试情况的统计,得到他在同类模拟考试中各题的得分率,如表所示:

假设学生甲每次考试各题的得分相互独立.
(1)若此项竞赛考试四道题的顺序依次为代数、几何、数论、组合,试预测学生甲考试得160分的概率;
(2)学生甲研究该项竞赛近五年的试题发现第1题都是代数题,于是他在赛前针对代数版块进行了强化训练,并取得了很大进步,现在,只要代数题是在试卷第1、2题的位置,他就一定能答对,若今年该项数学竞赛考试四道题的顺序依次为代数、数论、组合、几何,试求学生甲此次考试得分X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=sinωx(ω>0)向左平移![]() 个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)在(0,2π)上有且只有3个极大值点,f(x)在(0,2π)上有且只有2个极小值点
C.f(x)在![]() 上单调递增
上单调递增
D.ω的取值范围是[![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:
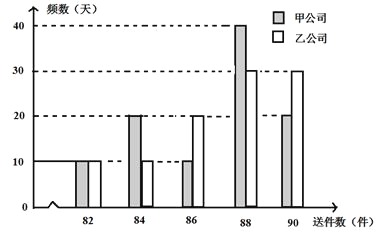
(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com