
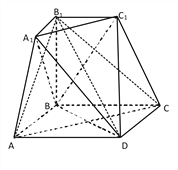
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.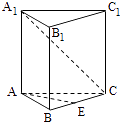
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中定义一种运算“⊙”,具有性质:①对任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③对任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)﹣2c,则函数f(x)=x⊙ ![]() 的最小值是( )
的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD. 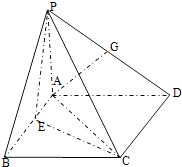
(1)求证:AG⊥平面PCD;
(2)求直线PD与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是 . (填写所有正确的序号) ①若sinx+siny= ![]() ,则siny﹣cos2x的最大值为
,则siny﹣cos2x的最大值为 ![]() ;
;
②函数y=sin(2x+ ![]() )的单调增区间是[kπ﹣
)的单调增区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
③函数f(x)= ![]() 是奇函数;
是奇函数;
④函数y=tan ![]() ﹣
﹣ ![]() 的最小正周期是π.
的最小正周期是π.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax﹣lnx,x∈(0,e],其中e是自然常数,a∈R.
(1)当a=1时,求f(x)的单调区间和极值;
(2)是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
(3)证明:(1﹣ ![]() )(
)( ![]() )(
)( ![]() ﹣
﹣ ![]() )…(
)…( ![]() ﹣
﹣ ![]() )<e3(3﹣n) .
)<e3(3﹣n) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx. 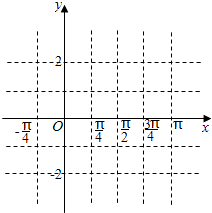
(1)当x∈[0, ![]() ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的简图;
]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某正弦交流电的电压v(单位V)随时间t(单位:s)变化的函数关系是v=120 ![]() sin(100πt﹣
sin(100πt﹣ ![]() ),t∈[0,+∞).
),t∈[0,+∞).
(1)求该正弦交流电电压v的周期、频率、振幅;
(2)若加在霓虹灯管两端电压大于84V时灯管才发光,求在半个周期内霓虹灯管点亮的时间?( 取 ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
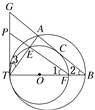
【题目】如图所示,两圆内切于点T,大圆的弦AB切小圆于点C.TA,TB与小圆分别相交于点E,F.FE的延长线交两圆的公切线TP于点P.
求证:(1) ![]() =
=![]() ;
;
(2)AC·PF=BC·PT.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com