
【题目】已知椭圆C: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点
=1(a>b>0)的左右焦点分别为F1 , F2 , 点 ![]() 为短轴的一个端点,∠OF2B=60°.
为短轴的一个端点,∠OF2B=60°.
(Ⅰ)求椭圆C的方程;
(Ⅱ)如图,过右焦点F2 , 且斜率为k(k≠0)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线AE,AD分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.试问kk′是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
【答案】解:(1)由条件可知 ![]() ,故所求椭圆方程为
,故所求椭圆方程为 ![]() .(2)设过点F2(1,0)的直线l方程为:y=k(x﹣1).
.(2)设过点F2(1,0)的直线l方程为:y=k(x﹣1).
由 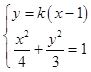 可得:(4k2+3)x2﹣8k2x+4k2﹣12=0
可得:(4k2+3)x2﹣8k2x+4k2﹣12=0
因为点F2(1,0)在椭圆内,所以直线l和椭圆都相交,即△>0恒成立.
设点E(x1 , y1),D(x2 , y2),
则 ![]() .
.
因为直线AE的方程为: ![]() ,直线AD的方程为:
,直线AD的方程为: ![]() ,
,
令x=3,可得 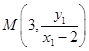 ,
, 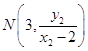 ,所以点P的坐标
,所以点P的坐标 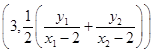 .
.
直线PF2的斜率为 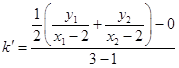 =
= 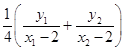 =
= ![]() =
= ![]() =
= 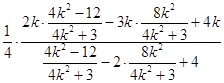
= ![]() ,
,
所以kk'为定值 ![]() .
.
【解析】(1)由条件可知 ![]() ,故求的椭圆方程.(2)设过点F2(1,0)的直线l方程为:y=k(x﹣1).由
,故求的椭圆方程.(2)设过点F2(1,0)的直线l方程为:y=k(x﹣1).由 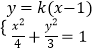 可得:(4k2+3)x2﹣8k2x+4k2﹣12=0.因为直线AE的方程为:
可得:(4k2+3)x2﹣8k2x+4k2﹣12=0.因为直线AE的方程为: ![]() ,直线AD的方程为:
,直线AD的方程为: ![]() ,从而列式求解即可.
,从而列式求解即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有一些大小相同的红球和黑球,从中取出2个球.两个球都是红球的概率是 ![]() ,都是黑球的概率是
,都是黑球的概率是 ![]() ,则取出的2个球中恰好一个红球一个黑球的概率是( )
,则取出的2个球中恰好一个红球一个黑球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A、B、C所对应的边为a,b,c. (I)若sin(A+ ![]() )=
)= ![]() cosA,求A的值;
cosA,求A的值;
(Ⅱ)若cosA= ![]() ,b=3c,求sinC的值.
,b=3c,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S表示所有大于﹣1的实数构成的集合,确定所有的函数:S→S,满足以下两个条件:
对于S内的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);在区间﹣1<x<0与x>0的每一个内, ![]() 是严格递增的.求满足上述条件的函数的方程.
是严格递增的.求满足上述条件的函数的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,a1=2,a3=18.数列{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{an},{bn}的通项公式;
(2)设Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….试比较Pn与Qn的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com