
设函数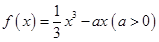 ,
,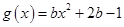 .
.
(1)若曲线 与
与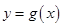 在它们的交点
在它们的交点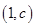 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值;
(2)当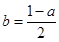 时,若函数
时,若函数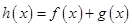 在区间
在区间 内恰有两个零点,求实数
内恰有两个零点,求实数 的取值范围;
的取值范围;
(3)当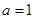 ,
,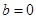 时,求函数
时,求函数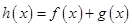 在区间
在区间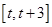 上的最小值.
上的最小值.
(1) ;(2)
;(2)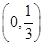 ;(3)
;(3) .
.
解析试题分析:(1)从条件“曲线
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
某地区注重生态环境建设,每年用于改造生态环境总费用为
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 与
与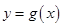 在它们的交点
在它们的交点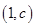 处有相同的切线”得到
处有相同的切线”得到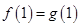 以及
以及 ,从而列有关
,从而列有关 、
、 的二元方程组,从而求出
的二元方程组,从而求出 与
与 的值;(2)将
的值;(2)将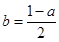 代入函数
代入函数 的解析式,利用导数分析函数
的解析式,利用导数分析函数 在区间
在区间 上的单调性,确定函数
上的单调性,确定函数 在区间
在区间 上是单峰函数后,然后对函数
上是单峰函数后,然后对函数 的端点值与峰值进行限制,列不等式组解出
的端点值与峰值进行限制,列不等式组解出 的取值范围;(3)将
的取值范围;(3)将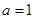 ,
,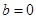 代入函数
代入函数 的解析式,并求出函数
的解析式,并求出函数 的单调区间,对函数
的单调区间,对函数 的极值点是否在区间
的极值点是否在区间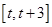 内进行分类讨论,结合函数的单调性确定函数
内进行分类讨论,结合函数的单调性确定函数 在区间
在区间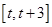 上的最小值.
上的最小值.
试题解析:(1)因为 ,
,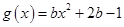 ,所以
,所以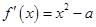 ,
,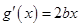 .
.
因为曲线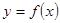 与
与 在它们的交点
在它们的交点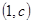 处有相同切线,
处有相同切线,
所以 ,且
,且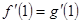 ,
,
即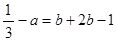 ,且
,且 ,解得
,解得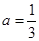 ,
, ;
;
(2)当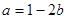 时,
时,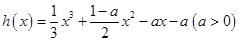 ,
,
所以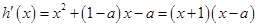 ,
,
令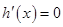 ,解得
,解得 ,
,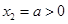 ,
,
当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:





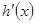
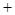

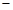

<


蓉城学堂阅读周练系列答案
文言文图解注译系列答案
课时配套练系列答案
全品高考复习方案系列答案
创意课堂中考总复习指导系列答案
举一反三完全训练系列答案
魔力导学案系列答案
绩优中考系列答案
课堂追踪系列答案
活力英语课课练与单元检测系列答案
 (
(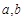 为常数),其图象是曲线
为常数),其图象是曲线 .
.
(1)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数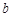 的取值范围;
的取值范围;
(3)已知点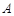 为曲线
为曲线 上的动点,在点
上的动点,在点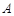 处作曲线
处作曲线 的切线
的切线 与曲线
与曲线 交于另一点
交于另一点 ,在点
,在点 处作曲线
处作曲线 的切线
的切线 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得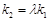 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.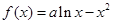 .
.
(1)当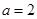 时,求函数
时,求函数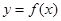 在
在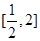 上的最大值;
上的最大值;
(2)令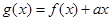 ,若
,若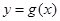 在区间
在区间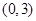 上不单调,求
上不单调,求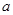 的取值范围;
的取值范围;
(3)当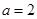 时,函数
时,函数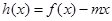 的图象与
的图象与 轴交于两点
轴交于两点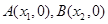 ,且
,且 ,又
,又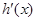 是
是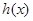 的导函数.若正常数
的导函数.若正常数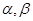 满足条件
满足条件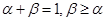 .证明:
.证明: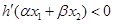 .
. 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 随每年改造生态环境总费用
随每年改造生态环境总费用 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用 的25%.
的25%.
若 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=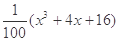 作为生态环境改造投资方案.
作为生态环境改造投资方案.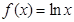 ,
,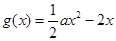 .
.
(Ⅰ)若曲线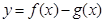 在
在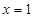 与
与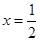 处的切线相互平行,求
处的切线相互平行,求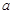 的值及切线斜率;
的值及切线斜率;
(Ⅱ)若函数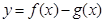 在区间
在区间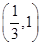 上单调递减,求
上单调递减,求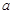 的取值范围;
的取值范围;
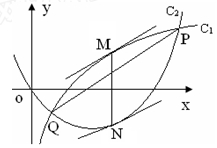
(Ⅲ)设函数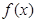 的图像C1与函数
的图像C1与函数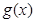 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行. ,函数
,函数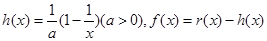 .
.
(I)试求f(x)的单调区间。
(II)若f(x)在区间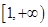 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围:
(III)设数列 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列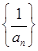 的前n项和为
的前n项和为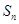 ,求证:当
,求证:当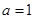 时,
时,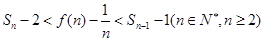 .
.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号