
【题目】已知函数f(x)=x2﹣2ax﹣2alnx(a∈R),则下列说法正确的是 ①当a<0时,函数y=f(x)有零点;
②若函数y=f(x)有零点,则a<0;
③存在a>0,函数y=f(x)有唯一的零点;
④若函数y=f(x)有唯一的零点,则a≤1.
【答案】①③④
【解析】解:令f(x)=x2﹣2ax﹣2alnx=0,则2a(x+lnx)=x2 , ∴2a= ![]() ,令g(x)=
,令g(x)= ![]() ,
,
则g′(x)=  =
= ![]()
令h(x)=x+lnx,通过作出两个函数y=lnx及y=﹣x的图像(如下图)
发现h(x)有唯一零点在(0,1)上,
设这个零点为x0 , 当x∈(0,x0)时,g′(x)<0,g(x)在(0,x0)上单调递减,x=x0是渐近线,
当x∈(x0 , 1)时,g′(x)<0,则g(x)在(x0 , 1)上单调递减,
当x∈(1,+∞)时g′(x)>0,g(x)在(1,+∞)单调递增,
∴g(1)=1,可以作出g(x)= ![]() 的大致图像,
的大致图像,
结合图像可知,当a<0时,y=2a与y=g(x)的图像只有一个交点,
则函数y=f(x)只有一个零点,故选项A正确;
若函数y=f(x)有零点,则a<0或a≥ ![]() ,故选项B不正确;
,故选项B不正确;
存在a= ![]() >0,函数y=f(x)有唯一零点,故选项C正确;
>0,函数y=f(x)有唯一零点,故选项C正确;
若函数y=f(x)有唯一零点,则a<0,或a= ![]() ,则a≤1,故选项D正确.
,则a≤1,故选项D正确.
所以答案是:①③④.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获纯利多少元?
已知: ![]() x
x ![]() =280,
=280, ![]() y
y ![]() =45309,
=45309, ![]() xiyi=3487,
xiyi=3487, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法,对于求一个n次多项式函数fn(x)=anxn+an﹣1xn﹣1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和 ![]() 乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
A.﹣5×3=﹣15
B.0.5×3+4=5.5
C.3×33﹣5×3=66
D.0.5×36+4×35=1336.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知☉O1与☉O2相交于A,B两点,过点A作☉O1的切线交☉O2于点C,过点B作两圆的割线,分别交☉O1、☉O2于点D、E,DE与AC相交于点P.若AD是☉O2的切线,且PA=6,PC=2,BD=9,则AB的长为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销该商品,可采用不同形式的分期付款,付款的期数![]() (单位:
(单位: ![]() )与商场经销一件商品的利润
)与商场经销一件商品的利润![]() (单位:元)满足如下关系:
(单位:元)满足如下关系: 
(Ⅰ)若记事件“购买该商品的3位顾客中,至少有1位采用一次性全额付款方式”为![]() ,试求事件
,试求事件![]() 的概率
的概率![]() ;
;
(Ⅱ)求商场经销一件商品的利润![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.将右边给出的程序框图补充完整,
(1)___________________ (2)_______________________
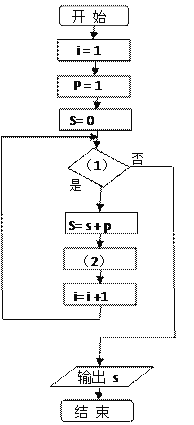
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班![]() 名学生在一次坐位体前屈测试中,成绩全部介于
名学生在一次坐位体前屈测试中,成绩全部介于![]() 与
与![]() 之间,将测试结果按如下方式分成五组:第一组
之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
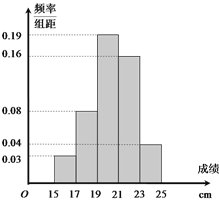
,…,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于![]() 且小于
且小于![]() 认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
(Ⅱ)若成绩之差的绝对值大于![]() 认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() :
:![]() (
(![]() 为参数),经过伸缩变换
为参数),经过伸缩变换![]() 后得到曲线
后得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)若点![]() 的曲线
的曲线![]() 上运动,试求出
上运动,试求出![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com