
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,
,![]() :实数
:实数![]() 满足
满足![]()
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)![]()
【解析】
试题分析:(1)根据题意可知,命题p,q分别表示一元二次不等式的解集,然后利用且命题为真,得到实数x的取值范围。
(2)根据p是q的充分不必要条件,表明q是p的充分不必要条件,利用集合的思想来求解得到。
(1) 当a>0时, {x|x2-4ax+3a2<0}={x|(x-3a)(x-a)<0}={x|a<x<3a},如果a=1时,则x的取值范围是{x|1<x<3},而{x|x2-x-6≤0,且x2+2x-8>0}={x|2<x≤3},
因为p∧q为真,所以有{x|1<x<3}∩{x|2<x≤3}={x|2<x<3}.故实数x的取值范围是{x|2<x≤3}.
(2) 若p是q的充分不必要条件,表明q是p的充分不必要条件.由(1)知,{x|2<x≤3}是{x|a<x<3a}(a>0)的真子集,易知a≤2且3<3a,解得{a|1<a≤2}.故实数a的取值范围是{a|1<a≤2}.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(2,0),点B在单位圆上,∠AOB=θ(0<θ<π).
(1)若点B(﹣ ![]() ,
, ![]() ),求tan(
),求tan( ![]() ﹣θ)的值;
﹣θ)的值;
(2)若 ![]() ,
, ![]()
![]() =
= ![]() ,求cos(
,求cos( ![]() +θ)的值.
+θ)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线ax+by—4=0和圆x2+y2=4没有公共点,则过点(a,b)的直线与椭圆![]() +
+![]() =1的公共点个数为( )
=1的公共点个数为( )
A. 0 B. 1 C. 2 D. 由a,b的取值来确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一动圆与定圆![]() 外切,同时和圆
外切,同时和圆![]() 内切,定点A(1,1).
内切,定点A(1,1).
(1)求动圆圆心P的轨迹E的方程,并说明是何种曲线;
(2)M为E上任意一点, F为E的左焦点,试求![]() 的最小值;
的最小值;
(3)试求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=(log2x)2﹣2alog2x+b(x>0).当x= ![]() 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.
(1)求a与b的值;
(2)求满足f(x)<0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,若
中,若![]() 是线段
是线段![]() 上的动点,则下列结论不正确的是( )
上的动点,则下列结论不正确的是( )
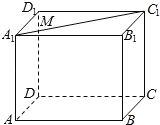
A. 三棱锥![]() 的正视图面积是定值
的正视图面积是定值
B. 异面直线![]() ,
,![]() 所成的角可为
所成的角可为![]()
C. 异面直线![]() ,
,![]() 所成的角为
所成的角为![]()
D. 直线![]() 与平面
与平面![]() 所成的角可为
所成的角可为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
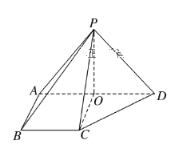
(1)求B点到平面PCD的距离;
(2)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com