
【题目】已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
【答案】(1)an=2n,n∈N*(2)1-![]() +n2
+n2
【解析】
(1)等比数列{an}的公比设为q,由等差数列中项性质和等比数列的通项公式,解方程可得q,进而得到所求通项公式;
(2)求得![]() =
=![]() +2log22n-1=
+2log22n-1=![]() +2n-1,由数列的分组求和和等差数列、等比数列的求和公式,计算可得所求和.
+2n-1,由数列的分组求和和等差数列、等比数列的求和公式,计算可得所求和.
(1)等比数列{an}的公比设为q,a1=2,
a1,a2,a3-2成等差数列,可得2a2=a1+a3-2,
即为4q=2+2q2-2,解得q=2,
则an=a1qn-1=2n,n∈N*;
(2)![]() =
=![]() +2log22n-1=
+2log22n-1=![]() +2n-1,
+2n-1,
则数列{bn}的前n项和Sn=(![]() +
+![]() +…+
+…+![]() )+(1+3+…+2n-1)
)+(1+3+…+2n-1)
=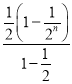 +
+![]() n(1+2n-1)=1-
n(1+2n-1)=1-![]() +n2.
+n2.


科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 与
与![]() 的图象拼成如图所示的“
的图象拼成如图所示的“![]() ”字形折线段
”字形折线段![]() ,不含
,不含![]()
![]()
![]()
![]()
![]() 五个点,若
五个点,若![]() 的图象关于原点对称的图形即为
的图象关于原点对称的图形即为![]() 的图象,则其中一个函数的解析式可以为__________.
的图象,则其中一个函数的解析式可以为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.

(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
其中
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,任取
,任取![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 最小值为
最小值为![]() 记
记![]() . 则关于函数
. 则关于函数![]() 有如下结论:
有如下结论:
①函数![]() 为偶函数;
为偶函数;
②函数![]() 的值域为
的值域为![]() ;
;
③函数![]() 的周期为2;
的周期为2;
④函数![]() 的单调增区间为
的单调增区间为![]() .
.
其中正确的结论有____________.(填上所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上钻石的重量计量单位为克拉;已知某种钻石的价值![]() (美元)与其重量
(美元)与其重量![]() (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若把一颗钻石切割成重量比为![]() 的两颗钻石,求价值损失的百分率;
的两颗钻石,求价值损失的百分率;
(3)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为![]() 克拉和
克拉和![]() 克拉,试用你所学的数学知识分析当
克拉,试用你所学的数学知识分析当![]() ,
,![]() 满足何种关系时,价值损失的百分率最大.
满足何种关系时,价值损失的百分率最大.
(注:价值损失的百分率![]() ,在切割过程中重量损耗忽略不计)
,在切割过程中重量损耗忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上给定![]() 及点
及点![]() ,构造点列
,构造点列![]() ,
,![]() ,
,![]() ,…,使得
,…,使得![]() 为点
为点![]() 绕中心
绕中心![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,而
时所到达的位置,而![]() 和
和![]() 为点
为点![]() 和
和![]() 分别绕中心
分别绕中心![]() 和
和![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,
时所到达的位置,![]() .若对某个
.若对某个![]() ,有
,有![]() ,试求
,试求![]() 的各个内角的度数及三个顶点
的各个内角的度数及三个顶点![]() ,
,![]() ,
,![]() 的排列方向.
的排列方向.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com