Question

已知双曲线C的中心在原点，抛物线y²=2x的焦点是双曲线C的一个焦点，且双曲线过点（1，）,

（1）求双曲线的方程；

（2）设直线l:y=kx+1与双曲线C交于A、B两点，试问：

①k为何值时⊥;

②是否存在实数k，使A、B两点关于直线y=mx对称（m为常数），若存在，求出k的值；若不存在，请说明理由.

Answer 1

解析：（1）由题意设双曲线方程为=1，

把（1，）代入得=1.                                                (*)

又y²=2x的焦点是（，0），故双曲线的c²=a²+b²=与（*）联立，消去b²可得4a²-21a²+5=0,(4a²-1)(a²-5)=0.

∴a²=,a²=5（不合题意舍去）

于是b²=1，∴双曲线方程为4x²-y²=1；

（2）由消去y得

（4-k²）x²-2kx-2=0.                                                          （*）

当Δ＞0 即-2＜k＜2(k≠±2)时，

l与C有两个交点A、B,

①设A（x₁，y₁）,B(x₂，y₂)，

因⊥，故·=0即x₁x₂+y₁y₂=0，

由（*）知x₁+x₂=,x₁x₂=，

代入可得+k²·+k·+1=0,

化简得k²=2,∴k=±，检验符合条件，故当k=±时，⊥.

②若存在实数k满足条件，则必须

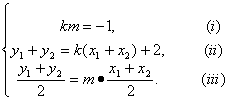
由(ⅱ)(ⅲ)得m(x₁+x₂)=k(x₁+x₂)+2,

把x₁+x₂=代入(ⅰ)得mk=4这与(ⅰ)的km=-1矛盾，故不存在实数k满足条件.