
【题目】一次测验共有4个选择题和2个填空题,每答对一个选择题得20分,每答对一个填空题得10分,答错或不答得0分,若某同学答对每个选择题的概率均为 ![]() ,答对每个填空题的概率均为
,答对每个填空题的概率均为 ![]() ,且每个题答对与否互不影响.
,且每个题答对与否互不影响.
(1)求该同学得80分的概率;
(2)若该同学已经答对了3个选择题和1个填空题,记他这次测验的得分为ξ,求ξ的分布列和数学期望.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x≥0时f(x)= ![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)的单调性(不必证明);
(3)若对任意的t∈R,不等式f(k﹣3t2)+f(t2+2t)≤0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨, ![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量, ![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(Ⅰ)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小;
的平均数与中位数的大小;
(Ⅱ)根据直方图估计利润![]() 不少于57万元的概率.
不少于57万元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线 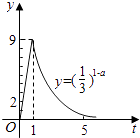
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 ![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩转盘游戏,该游戏规则是这样的:一个质地均匀的标有12等分数字格的转盘(如图),甲、乙两人各转转盘一次,转盘停止时指针所指的数字为该人的得分.(假设指针不能指向分界线)现甲先转,乙后转,求下列事件发生的概率 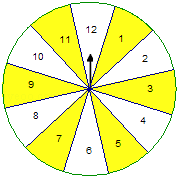
(1)甲得分超过7分的概率.
(2)甲得7分,且乙得10分的概率
(3)甲得5分且获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() 的焦点为F,直线
的焦点为F,直线![]() 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求C的方程;
(2)过F的直线![]() 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线![]() 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com