Question

【题目】如图，矩形ABCD是某小区户外活动空地的平面示意图，其中AB＝50米，AD＝100米，现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐（其中，点O为AD的中点，OM⊥ON，点M在AB上，点N在CD上），将破旧的道路AM重新铺设．已知草坪成本为每平方米20元，新道路AM成本为每米500元，设∠OMA＝θ，记草坪栽植与新道路铺设所需的总费用为f(θ)．

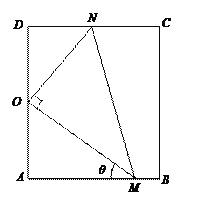
（1）求f(θ)关于θ函数关系式，并写出定义域；

（2）为节约投入成本，当tanθ为何值时，总费用 f(θ)最小？

Answer 1

【答案】（1）f(θ)＝，其定义域为；（2）

【解析】试题分析：（1）在RtOAM中，解出，在RtODN中求出ON＝，故可得，由题意当点M与点B重合时，θ取最小值；当点N与点C重合时，θ取最大值，即，故可得最后结果；（2）由（1）可得，对其求导，利用导数判断其单调性得其最值.

试题解析：（1）据题意，在RtOAM中，OA＝50，∠OMA＝θ，所以AM＝，OM＝，据平面几何知识可知∠DON＝θ，在RtODN中，OD＝50，∠DON＝θ，所以ON＝，所以f(θ)＝＝＝ ，据题意，当点M与点B重合时，θ取最小值；当点N与点C重合时，θ取最大值，所以，所以f(θ)＝，其定义域为．

（2）由（1）可知，f(θ)＝， ， ＝＝＝，

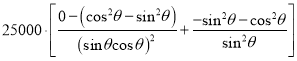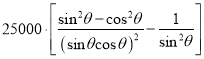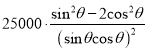令＝0，得，其中，列表：

θ
		↘	极小值	↗

所以当时，总费用 f(θ)取最小值，可节约投入成本．