
分析 根据已知等式,得到sin2β=-2sin2α+2sinα≥0,可以解出sinα的取值范围是[0,1],并且cos2β=1-sin2β=2sin2α-2sinα+1,结合cos2α=1-sin2α,代入cos2α+cos2β得关于sinα的二次函数:y═(sinα-1)2+1,其中sinα∈[0,1],由此能求出cos2α+cos2β的取值范围.
解答 解:∵2sin2α+sin2β-2sinα=0,
∴sin2β=-2sin2α+2sinα≥0,
可得0≤sinα≤1,cos2β=1-sin2β=2sin2α-2sinα+1
∴cos2α+cos2β=(1-sin2α)+(2sin2α-2sinα+1)
=2-2sinα+sin2α=(sinα-1)2+1.
∵0≤sinα≤1,
∴当sinα=0时,cos2α+cos2β有最大值为2,
当sinα=1时,cos2α+cos2β有最小值1.
∴1≤cos2α+cos2β≤2.
∴cos2α+cos2β的取值范围为[1,2].
故答案为:[1,2].
点评 本题考查两角余弦值平方和的取值范围的求法,是中档题,解题时要认真审题,注意同角三角函数关系式的合理运用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | $\frac{1}{{a{b^2}}}$<$\frac{1}{{{a^2}b}}$ | C. | a2b<ab2 | D. | $\frac{b}{a}$<$\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
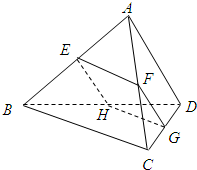 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:
一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com