
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
分析 解方程x2-ax-x+a=0得,x=a,或1,所以要求集合A需讨论a和1的关系:a<1时,A={x|x≥1,或x≤a},此时A∪B=R;a=1时,A=R,满足A∪B=R;a>1时,A={x|x≥a,或x≤1},要使A∪B=R,则0<a-1≤1,所以1<a≤2,对以上几种情况求得的a的取值范围求并集即可.
解答 解:解x2-(a+1)x+a=0得,x=a,或1;
①若a<1,则A={x|x≥1,或x≤a},B={x|x≥a-1};
∵a-1<a,则A∪B=R;
②若a=1,则A=R,满足A∪B=R;
③若a>1,则A={x|x≥a,或x≤1},要使A∪B=R,则:a-1≤1,∴1<a≤2;
∴综上得a≤2,即实数a的取值范围为(-∞,2].
故选:B.
点评 考查解一元二次方程,解一元二次不等式,以及利用数轴解决集合问题的方法.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:选择题
为了得到函数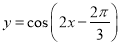 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向左平移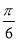 个单位长度
个单位长度
B.向左平移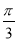 个单位长度
个单位长度
C.向右平移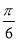 个单位长度
个单位长度
D.向右平移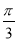 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(1,4)内有且仅有一个零点 | B. | 在(1,4)内至少有一个零点 | ||
| C. | 在(1,4)内至多有一个零点 | D. | 在(1,4)内不一定有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图点O在△ABC外部(O,A在直线BC的异侧),△ABC与△OBC的面积之比为1:3;记$\overrightarrow{AO}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$,则λ12+λ22的最小值为( )
如图点O在△ABC外部(O,A在直线BC的异侧),△ABC与△OBC的面积之比为1:3;记$\overrightarrow{AO}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$,则λ12+λ22的最小值为( )| A. | 16 | B. | $\frac{16}{9}$ | C. | 8 | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com