
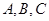 所对的边分别为
所对的边分别为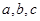 ,
,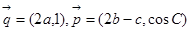 且
且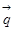 ∥
∥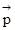
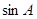 的值
的值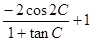 的取值范围
的取值范围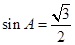 ;(Ⅱ)三角函数式
;(Ⅱ)三角函数式 的取值范围为(-1,
的取值范围为(-1, ].
].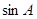 的值,可考虑利用正弦定理,也可利用面积公式
的值,可考虑利用正弦定理,也可利用面积公式 ,但本题由已知
,但本题由已知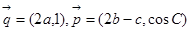 且
且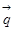 ∥
∥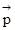 ,可根据向量平行的充要条件列式:
,可根据向量平行的充要条件列式: ,结合正弦定理与正弦的诱导公式,两角和的正弦公式化简整理,化简可得
,结合正弦定理与正弦的诱导公式,两角和的正弦公式化简整理,化简可得 ,可得
,可得 ,从而得到
,从而得到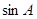 的值;(II)求三角函数式
的值;(II)求三角函数式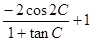 的取值范围,将三角函数式用二倍角的余弦公式结合“切化弦”,化简整理得
的取值范围,将三角函数式用二倍角的余弦公式结合“切化弦”,化简整理得 ,再根据
,再根据 算出
算出 的范围,得到
的范围,得到 的取值范围,最终得到原三角函数式的取值范围.
的取值范围,最终得到原三角函数式的取值范围.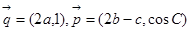 且
且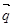 ∥
∥ ,∴
,∴
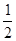 sinC=cosAsinC
sinC=cosAsinC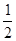 ,
, , ∴
, ∴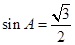
 +1=1-
+1=1- =1-2cos2C+2sinCcosC=sin2C-cos2C=
=1-2cos2C+2sinCcosC=sin2C-cos2C=
 p ∴
p ∴ <2C-
<2C- <
< , ∴
, ∴ < sin(2C-
< sin(2C- )≤1
)≤1 sin(2C-
sin(2C- )≤
)≤ , 即三角函数式
, 即三角函数式 的取值范围为(-1,
的取值范围为(-1, ]
]

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com