
【题目】已知![]() ,
, ![]() 为椭圆
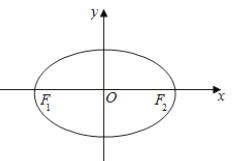
为椭圆![]() :
: ![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 的面积为1,
的面积为1, ![]() (
(![]() ,
, ![]() ),当点
),当点![]() 在椭圆
在椭圆![]() 上运动时,试问
上运动时,试问![]() 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出![]() 的取值范围.
的取值范围.
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
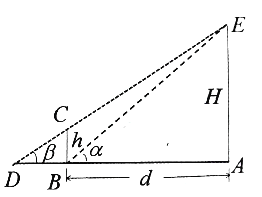
【题目】莫数学建模兴趣小组测量某移动信号塔![]() 的高度
的高度![]() (单位:
(单位: ![]() ),如图所示,垂直放置的标杆
),如图所示,垂直放置的标杆![]() 的高度
的高度![]() ,仰角
,仰角![]() ,
, ![]() .
.
(Ⅰ)该小组已经测得一组![]() 的值,
的值, ![]() ,
, ![]() ,请推测
,请推测![]() 的值;
的值;
(Ⅱ)该小组对测得的多组数据分析后,发现适当调节标杆到信号塔的距离![]() (单位:
(单位: ![]() ),使得
),使得![]() 较大时,可以提高信号塔测量的精确度,若信号塔高度为
较大时,可以提高信号塔测量的精确度,若信号塔高度为![]() ,试问
,试问![]() 为多大时,
为多大时, ![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=x,g(x)= ![]()
D.f(x)=1,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4, 则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 (x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 (x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中, 随机抽取2件产品,
(ⅰ) 用产品编号列出所有可能的结果;
(ⅱ) 设事件B为“在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是实数,f(x)=a﹣ ![]() (x∈R).
(x∈R).
(1)证明不论a为何实数,f(x)均为增函数;
(2)若f(x)满足f(﹣x)+f(x)=0,解关于x的不等式f(x+1)+f(1﹣2x)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com