
����Ŀ��ij��˾������Ϊ���������ܷ����ٰ취��֪ʶ�ʴ�������Ը���18��68�����Ⱥ��ȡһ������Ϊn�������������������ݷֳ����飺[18��28����[28��38����[38��48����[48��58����[58��68�����ٽ��䰴�����ҵ�˳��ֱ���Ϊ��1�飬��2�飬������5�飬������������Ƶ�ʷֲ�ֱ��ͼ�����Իش������������ͳ�ƺ�����±���ʾ��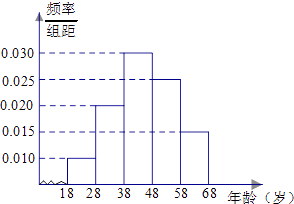
��� | ���� | �ش���ȷ������ | �ش���ȷ������ռ����ı��� |
��1�� | [18��28�� | 5 | 0.5 |
��2�� | [28��38�� | 18 | a |
��3�� | [38��48�� | 27 | 0.9 |
��4�� | [48��58�� | x | 0.36 |
��5�� | [58��68�� | 3 | 0.2 |
��1���ֱ����a��x��ֵ��
��2���ӵ�2��3��4��ش���ȷ�������÷ֲ����������ȡ6�ˣ����2��3��4��ÿ��Ӧ����ȡ�����ˣ�
��3���ڣ�2����ǰ���£�����������ȡ��6���������ȡ2�˰䷢���˽���������ȡ�����е�2��������1�˻�����˽��ĸ��ʣ�
���𰸡�
��1���⣺��1������5��0.5=10������n=10��0.1=100��
��2��Ƶ��Ϊ��0.2������Ϊ��100��0.2=20������a=18��20=0.9��
��4������100��0.25=25������x=25��0.36=9
��2���⣺��2��3��4��ش���ȷ���˵ı�Ϊ18��27��9=2��3��1�����Ե�2��3��4��ÿ��Ӧ�����γ�ȡ2�ˣ�3�ˣ�1�ˣ�
��3���⣺�ǡ�����ȡ�����е�2��������1�˻�����˽���Ϊ�¼�A����ȡ��6���У���2�����Ϊa1��a2����3�����Ϊb1��b2��b3����4�����Ϊc�����6������������ȡ2�������п��ܵ������15�֣������ǣ���a1��a2������a1��b1������a1��b2������a1��b3������a1��c������a2��b1������a2��b2������a2��b3������a2��c������b1��b2������b1��b3������b1��c������b2��b3������b2��c������b3��c����
���е�2��������1�˵������9�֣������ǣ���a1��a2������a1��b1������a1��b2������a1��b3������a1��c������a2��b1����
��a2��b2������a2��b3������a2��c����
��P��A��= ![]() ��
��
������ȡ�����е�2��������1�˻�����˽��ĸ���Ϊ ![]()
����������1�����ݻش�Ե�����:ÿ�������=�ش���ȷ�ĸ��ʣ��ֱ�����Ҫ���ֵ����2���ɷֲ������������ȡ���ص�ɵø������������3���dz�ȡ��6���У���2��ļ�Ϊa1��a2����3�����Ϊb1��b2��b3����4�����Ϊc���оٿɵô�6��ѧ������ȡ2�������п��ܵ�������Լ����е�2��������1�˵�����������ɹŵ���Ϳɵø���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2ex��1+ax3+bx2 �� ��֪x=��2��x=1Ϊf��x���ļ�ֵ�㣮
��1����a��b��ֵ��
��2������f��x���ĵ����ԣ�
��3����g��x��= ![]() x3��x2 �� �ԱȽ�f��x����g��x���Ĵ�С��
x3��x2 �� �ԱȽ�f��x����g��x���Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��n��=1+ ![]() +
+ ![]() +
+ ![]() +��+
+��+ ![]() ��g��n��=
��g��n��= ![]() ��
�� ![]() ��n��N* ��
��n��N* ��
��1����n=1��2��3ʱ���ԱȽ�f��n����g��n���Ĵ�С��ϵ��
��2������f��n����g��n���Ĵ�С��ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4���±�ҵ����ʦҪ���䵽����ѧУ�ν̣�ÿ����ʦ���з��䣨��������ֱ�ʾ����
��1�����ж����ֲ�ͬ�ķ��䷽����
��2��ǡ��һ��ѧУ��������ʦ���ж����ֲ�ͬ�ķ��䷽����
��3��ij��ѧУ������2����ʦ���ж����ֲ�ͬ�ķ��䷽����
��4��ǡ������ѧУ��������ʦ���ж����ֲ�ͬ�ķ��䷽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}����a1=1����an+1��an=n+1��n��N*����������{ ![]() }��ǰ10��ĺ�Ϊ ��
}��ǰ10��ĺ�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪F����ԲC�� ![]() +
+ ![]() =1���ҽ��㣬P��C��һ�㣬A����2��1��������APF�ܳ���Сʱ�������Ϊ ��
=1���ҽ��㣬P��C��һ�㣬A����2��1��������APF�ܳ���Сʱ�������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��������ֵ��x1 �� x2 �� ��x1��x2 �� �ǵ�M��x1 �� f��x1������N��x2 �� f��x2������
��������ֵ��x1 �� x2 �� ��x1��x2 �� �ǵ�M��x1 �� f��x1������N��x2 �� f��x2������
������ֱ��MN�ķ��̣�
����֤�����߶�MN������y=f��x������ֻ��һ������M��N�Ĺ����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=x3��6x2+9x��abc��a��b��c����f��a��=f��b��=f��c��=0���ָ������½��ۣ�
��f��0��f��1����0��
��f��0��f��1����0��
��f��0��f��3����0��
��f��0��f��3����0��
������ȷ���۵�����ǣ� ��
A.�٢�
B.�٢�
C.�ڢ�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y= ![]() +lg����x2+4x��3���Ķ�����ΪM��
+lg����x2+4x��3���Ķ�����ΪM��
��1����M��
��2����x��Mʱ������f��x��=a2x+2+34x��a����3������Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com