
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本
万元(总成本![]() 固定成本
固定成本![]() 生产成本).销售收入
生产成本).销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入
销售收入![]() 总成本);
总成本);
(2)工厂生产多少台产品时,可使盈利最多?
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(2x-x2)ex
①(-![]() ,
,![]() )是f(x)的单调递减区间;
)是f(x)的单调递减区间;
②f(-![]() )是f(x)的极小值,f(
)是f(x)的极小值,f(![]() )是f(x)的极大值;
)是f(x)的极大值;
③f(x)没有最大值,也没有最小值;
④f(x)有最大值,没有最小值.
其中判断正确的是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
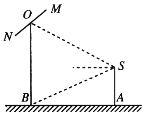
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-sin2x+mcosx-1,x∈[![]() ].
].
(1)若f(x)的最小值为-4,求m的值;
(2)当m=2时,若对任意x1,x2∈[-![]() ]都有|f(x1)-f(x2)|
]都有|f(x1)-f(x2)|![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com