
【题目】已知函数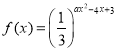 ,
,
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 有最大值3,求
有最大值3,求![]() 的值.
的值.
(3)若![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)函数f(x)的递增区间是(2,+∞),递减区间是(∞,2);(2)a=1;(3){0}
【解析】
(1)当a=1时, ,令
,令![]() ,结合指数函数的单调性,二次函数的单调性和复合函数的单调性,可得f(x)的单调区间;
,结合指数函数的单调性,二次函数的单调性和复合函数的单调性,可得f(x)的单调区间;
(2)令![]() ,
,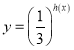 ,由于f(x)有最大值3,所以 h(x)应有最小值1,进而可得a的值.
,由于f(x)有最大值3,所以 h(x)应有最小值1,进而可得a的值.
(3)由指数函数的性质知,要使y=h(x)的值域为(0,+∞).应使![]() 的值域为R,进而可得a的取值范围.
的值域为R,进而可得a的取值范围.
(1)当a=1时,  ,
,
令![]() ,
,
由于g(x)在(∞,2)上单调递增,在(2,+∞)上单调递减,
而![]() 在R上单调递减,
在R上单调递减,
所以f(x)在(∞,2)上单调递减,在(2,+∞)上单调递增,
即函数f(x)的递增区间是(2,+∞),递减区间是(∞,2).
(2)令![]() ,
,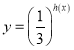 ,由于f(x)有最大值3,
,由于f(x)有最大值3,
所以h(x)应有最小值1,
因此![]() =1,
=1,
解得a=1.
即当f(x)有最大值3时,a的值等于1.
(3)由指数函数的性质知,
要使y=h(x)的值域为(0,+∞).
应使![]() 的值域为R,
的值域为R,
因此只能有a=0.
因为若a≠0,则h(x)为二次函数,其值域不可能为R.
故a的取值范围是{0}.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在199319936688张卡片上,每张写上一个自然数,恰写了1,2,…,199319936688这199319936688个自然数.问能否把这些卡片分成三组,使得第二组卡片上写的数之总和比第一组卡片上写的数之总和大33,而第三组卡片上写的数之总和比第二组卡片上写的数之总和大102?
若能,请给出一种分组方法.若不能,请你说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出函数![]() 如下表,则f〔g(x)〕的值域为( )
如下表,则f〔g(x)〕的值域为( )
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,通过抽样,得到100位员工每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如图.
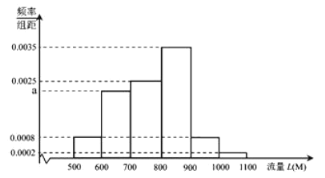
(1)从该企业的100位员工中随机抽取1人,求手机月平均使用流量不超过900M的概率;
(2)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
A | 20 | 700 |
B | 30 | 1000 |
流量套餐的规则是:每月1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含200M的流量)需要10元,可以多次购买,如果当月流量有剩余,将会被清零.该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用![]() 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为![]() 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:厘米)满足关系:
(单位:厘米)满足关系:![]() .若不建隔热层,每年的能源消耗费用为
.若不建隔热层,每年的能源消耗费用为![]() 万元.设
万元.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 最小,并求其最小值.
最小,并求其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com