Question

14．船上两根高5m的桅杆相距10m，一条30m长的绳子两端系在桅杆的顶上，并按如图所示的方式绷紧，假设绳子位于两根桅杆所在的平面内，求绳子与甲板接触点P到桅杆AB的距离．

Answer 1

分析 以两根桅杆的顶端A，C所在直线为x轴，线段AC的垂直平分线为y轴，建立如图所示直角坐标系，求出椭圆的方程，然后求解P到桅杆AB的距离．

解答 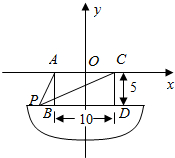解：以两根桅杆的顶端A，C所在直线为x轴，线段AC的垂直平分线为y轴，建立如图所示直角坐标系，…（2分）
则P点在以A，C为焦点的椭圆上，依题意，此椭圆的方程为$\frac{x^2}{225}+\frac{y^2}{200}=1$，…（8分）
因为P点纵坐标为-5，代入椭圆方程可解得$P（{-\frac{{15\sqrt{14}}}{4}，-5}）$…（12分）
所以P到桅杆AB的距离为$\frac{{15\sqrt{14}}}{4}-5$m．…（14分）
答：绳子与甲板接触点P到桅杆AB的距离为$\frac{{15\sqrt{14}}}{4}-5$m．…（16分）

点评 本题考查椭圆的标准方程的求法与应用，考查分析问题解决问题的能力．